题目内容
11. 如图所示,质量为m的小球用长为L的细线悬挂而静止在竖直位置,现用水平力F将小球缓慢地拉到细线与竖直方向成θ角的位置,重力加速度为g,则在此过程中拉力F做的功是( )
如图所示,质量为m的小球用长为L的细线悬挂而静止在竖直位置,现用水平力F将小球缓慢地拉到细线与竖直方向成θ角的位置,重力加速度为g,则在此过程中拉力F做的功是( )| A. | FLsinθ | B. | FLcosθ | C. | mgL(l-sinθ) | D. | mgL(l-cosθ) |
分析 小球从平衡位置P点缓慢移动到Q点,对小球受力分析,受重力、拉力F和绳子的拉力T,根据平衡条件求解出拉力的一般表达式,得出拉力为变力;再根据动能定理列式求解
解答 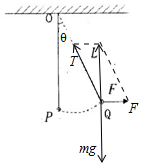 解:对小球受力分析,受到重力、拉力F和绳子的拉力T,如图,根据共点力平衡条件,有:
解:对小球受力分析,受到重力、拉力F和绳子的拉力T,如图,根据共点力平衡条件,有:
F=mgtanθ,
故F随着θ的增大而不断变大,故F是变力;对小球运动过程运用动能定理,得到:
-mgL(1-cosθ)+W=0
故拉力做的功等于mgL(1-cosθ)
故选:D
点评 本题关键在于拉力F是变力,求解变力做功可以根据动能定理列式求解

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
2.在电能输送过程中,若输送的电功率一定,则在输电线上损失的电功率( )
| A. | 随输电线电阻的增大而增大 | B. | 和输送电压的平方成正比 | ||
| C. | 和输电线上电压降落的平方成正比 | D. | 和输电线中电流强度的平方成正比 |
19.下列关于行星绕太阳运动的说法中,正确的是( )
| A. | 所有行星都在同一椭圆轨道上绕太阳运动 | |
| B. | 行星绕太阳运动的速率不变 | |
| C. | 行星绕太阳运动时太阳位于行星轨道的焦点处 | |
| D. | 所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等 |
6.下列关于万有引力定律的说法,正确的是( )
| A. | 万有引力定律是卡文迪许发现的 | |
| B. | 万有引力定律公式F=G$\frac{Mm}{{r}^{2}}$中的G是一个比例常数,是没有单位的 | |
| C. | 万有引力定律适用于自然界中的任何两个物体之间 | |
| D. | 万有引力定律公式F=G$\frac{Mm}{{r}^{2}}$表明当r等于零时,万有引力为无穷大 |
16. 如图所示,质量为m的小球从地面上方H高处无初速释放,落在地面后出现一个深度为h的坑,设地面对小球的阻力为恒力,重力加速度为g,则在整个运动过程中( )
如图所示,质量为m的小球从地面上方H高处无初速释放,落在地面后出现一个深度为h的坑,设地面对小球的阻力为恒力,重力加速度为g,则在整个运动过程中( )
 如图所示,质量为m的小球从地面上方H高处无初速释放,落在地面后出现一个深度为h的坑,设地面对小球的阻力为恒力,重力加速度为g,则在整个运动过程中( )
如图所示,质量为m的小球从地面上方H高处无初速释放,落在地面后出现一个深度为h的坑,设地面对小球的阻力为恒力,重力加速度为g,则在整个运动过程中( )| A. | 小球的重力势能减少了mgH | B. | 小球合外力对物体做的总功为零 | ||
| C. | 地面对小球阻力做的功为-mg(H+h) | D. | 地面对小球阻力做的功为-mgh |
3. 在抗洪抢险中,战士驾驶摩托艇救人,假设江岸是平直的,洪水沿江向下游流去,水流速度为v1,摩托艇在静水中的航速为v2,战士救人的地点A离岸边最近处O的距离为d,如战士想在最短时间内将人送上岸,则摩托艇登陆的地点离O点的距离为( )
在抗洪抢险中,战士驾驶摩托艇救人,假设江岸是平直的,洪水沿江向下游流去,水流速度为v1,摩托艇在静水中的航速为v2,战士救人的地点A离岸边最近处O的距离为d,如战士想在最短时间内将人送上岸,则摩托艇登陆的地点离O点的距离为( )
 在抗洪抢险中,战士驾驶摩托艇救人,假设江岸是平直的,洪水沿江向下游流去,水流速度为v1,摩托艇在静水中的航速为v2,战士救人的地点A离岸边最近处O的距离为d,如战士想在最短时间内将人送上岸,则摩托艇登陆的地点离O点的距离为( )
在抗洪抢险中,战士驾驶摩托艇救人,假设江岸是平直的,洪水沿江向下游流去,水流速度为v1,摩托艇在静水中的航速为v2,战士救人的地点A离岸边最近处O的距离为d,如战士想在最短时间内将人送上岸,则摩托艇登陆的地点离O点的距离为( )| A. | $\frac{d{v}_{2}}{\sqrt{{v}_{2}^{2}}-{v}_{1}^{2}}$ | B. | 0 | C. | $\frac{d{v}_{1}}{{v}_{2}}$ | D. | $\frac{d{v}_{2}}{{v}_{1}}$ |
13. 如图所示,在区域Ⅰ和区域Ⅱ内分别存在与纸面垂直的匀强磁场,一带电粒子沿着弧线apb由区域I运动到区域Ⅱ.已知圆弧ap与圆弧pb的弧长之比为2:1,下列说法正确的是( )
如图所示,在区域Ⅰ和区域Ⅱ内分别存在与纸面垂直的匀强磁场,一带电粒子沿着弧线apb由区域I运动到区域Ⅱ.已知圆弧ap与圆弧pb的弧长之比为2:1,下列说法正确的是( )
 如图所示,在区域Ⅰ和区域Ⅱ内分别存在与纸面垂直的匀强磁场,一带电粒子沿着弧线apb由区域I运动到区域Ⅱ.已知圆弧ap与圆弧pb的弧长之比为2:1,下列说法正确的是( )
如图所示,在区域Ⅰ和区域Ⅱ内分别存在与纸面垂直的匀强磁场,一带电粒子沿着弧线apb由区域I运动到区域Ⅱ.已知圆弧ap与圆弧pb的弧长之比为2:1,下列说法正确的是( )| A. | 粒子在区域I和区域II中的速率之比为2:1 | |
| B. | 粒子通过圆弧ap、pb的时间之比为2:1 | |
| C. | 圆弧ap与圆弧pb对应的圆心角之比为2:1 | |
| D. | 区域I和区域II的磁感应强度方向相反 |
 如图所示,一定质量的理想气体被活塞封闭在竖直放置的高为2h圆柱形气缸内,气缸壁导热良好,活塞可沿气缸壁无摩擦地滑动.开始时气柱高度为h,将气缸倒转过来,再次平衡后气柱高度变为$\frac{3}{2}$h.保持气体温度不变,已知大气压强P0,气缸横截面积为S,重力加速度为g.求:活塞的质量M.
如图所示,一定质量的理想气体被活塞封闭在竖直放置的高为2h圆柱形气缸内,气缸壁导热良好,活塞可沿气缸壁无摩擦地滑动.开始时气柱高度为h,将气缸倒转过来,再次平衡后气柱高度变为$\frac{3}{2}$h.保持气体温度不变,已知大气压强P0,气缸横截面积为S,重力加速度为g.求:活塞的质量M.