题目内容
(13分)如图甲所示,斜面体固定在粗糙的水平地面上,底端与水平面平滑连接,一个可视为质点的物块从斜面体的顶端自由释放,其速率随时间变化的图像如图乙所示,(已知斜面与物块、地面与物块的动摩擦因数相同,g取10m/s2)求: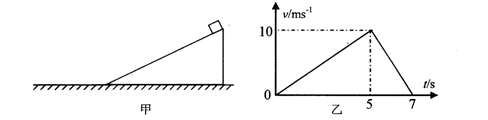
⑴斜面的长度s;
⑵物块与水平面间的动摩擦因数μ;
⑶斜面的倾角θ的正弦值.
⑴s=25m;⑵μ=0.5;⑶sinθ=0.6
解析试题分析:⑴在v-t图象中图线与时间轴所围的面积表示了物体的位移,由v-t图象可知,物块在0~5s时间内在斜面上运动,5~7s时间内在水平面上运动,因此斜面的长度为:s= ×5×10m=25m
×5×10m=25m
⑵在v-t图象中图线的斜率表示了物体运动的加速度,因此由v-t图象可知,在5~7s时间内,该物块运动的加速度为:a2=-5m/s2
物块在水平面上运动时,根据牛顿第二定律有:-μmg=ma2
解得:μ=0.5
⑶同理,在0~5s时间内物块运动的加速度为:a1=2m/s2
根据牛顿第二定律有:mgsinθ-μmgcosθ=ma1
又因为:sin2θ+cos2θ=1
联立以上三式解得:sinθ=0.6
考点:本题主要考查了匀变速直线运动规律、牛顿第二定律以及v-t图象的理解与应用问题,属于中档题。

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 的光滑楔形滑块A上的顶端O处,细线另一端栓一质量为
的光滑楔形滑块A上的顶端O处,细线另一端栓一质量为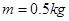 的小球,取
的小球,取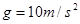 .
.
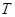 等于多少?
等于多少?