题目内容
如图所示,质量M=1kg的木板静止在粗糙的水平地面上,木板与地面间的动摩擦因数μ1=0.1,在木板的左端放置一个质量m=1kg,大小可忽略的铁块,铁块与木板间的动摩擦因数μ2=0.4,g取10m/s2,试求: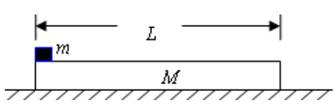
(1)若木板长L=1m,在铁块上加一个水平向右的恒力F=8N,经过多长时间铁块运动到木板的右端?
(2)若在铁块右端施加一个从零开始连续增大的水平向右的力F,假设木板足够长,在图中画出铁块受到木板的摩擦力f2随拉力F大小的变化而变化的图象。
(1)1s (2)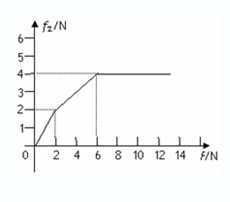
解析试题分析:(1)由牛顿第二定律:木块的加速度大小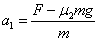 =4m/s2
=4m/s2
木板的加速度大小 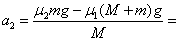 2m/s2
2m/s2
设经过时间t铁块运动到木板的右端,则有 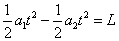 解得:t="1s" (3分)
解得:t="1s" (3分)
(2)铁块与木板间的最大静摩擦力为:f=μmg=4N,
木板与地面间的最大静摩擦力为:F`= μ1(mg+Mg)=2N
①当F≤ μ1(mg+Mg)=2N时,A、B相对静止且对地静止,f2="F" (2分)
②当F≥2N时,设AB恰好保持相对静止(AB间的静摩擦力大达到最大)时的力为F,
以系统为研究对象,由牛顿第二定律:F-μ1(M+m)g=(M+m)a
以M为研究对象,由牛顿第二定律:f2-μ1(M+m)g=Ma
联立解得:a=2m/s2 F=6N,
所以当2N ≤ F ≤ 6N时,M、m相对静止,一起做匀加速直线运动,
加速度a=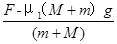 =
=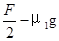 =
=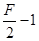
f2=μ1(M+m)g+Ma=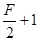
③当F>6N,A、B发生相对运动,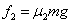 =4N
=4N
画出f2随拉力F大小变化的如图(2分)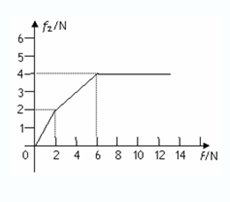
考点:本题考查牛顿运动定律的综合应用。

汽车起动的快慢和能够达到的最大速度,是衡量汽车性能的指标体系中的两个重要指标。汽车起动的快慢用车的速度从0到100km/h的加速时间来表示,这个时间越短,汽车起动的加速度就越大。下表中列出了两种汽车的性能指标(为了简化计算,把100km/h取为30m/s)。
| | 起动的快慢(单位:s) (0~30m/s的加速时间) | 最大速度(m/s) |
| 甲车 | 12 | 40 |
| 乙车 | 6 | 50 |
(1)甲、乙两车的起动加速度分别是多少?
(2)相遇时乙车发生的位移是多少?
(3)甲车比乙车提前运动的时间为多少?
 角的斜向下的推力
角的斜向下的推力 推一个重
推一个重 的箱子匀速前进,箱子与地面间的动摩擦因数为
的箱子匀速前进,箱子与地面间的动摩擦因数为 (
( )。求:
)。求:
 后撤去,箱子最远运动多长距离.
后撤去,箱子最远运动多长距离.

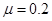 。从t=0开始,物体受到一个大小和方向呈周期性变化的水平力F的作用,力F 随时间的变化规律如图9所示。重力加速度
。从t=0开始,物体受到一个大小和方向呈周期性变化的水平力F的作用,力F 随时间的变化规律如图9所示。重力加速度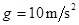 , 求:
, 求:
 的大小和方向;
的大小和方向; 时物块运动的瞬时速度
时物块运动的瞬时速度 的大小和方向;
的大小和方向;