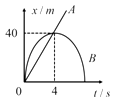
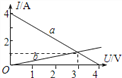
��Ŀ����
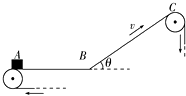
����Ŀ���뾶R=0.9m���ķ�֮һԲ���ι⻬�����ֱ���ã�Բ����͵�B�볤ΪL=1m��ˮƽ��������B�㣬BC������h=0.45m��C����һ���Ϊ��=30��Ĺ⻬б�����ӣ�����m=1.0kg��С�����Բ������D�ɾ�ֹ�ͷţ���֪������ˮƽ���Ķ�Ħ������=0.1��ȡg=10m/s2 �� ��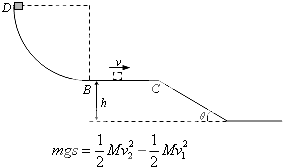
��1��С����յ���Բ����B��ʱ���ٶȺ�B�㴦��Բ����ѹ����
��2��С�����C���˶������������ʱ�䣮
���𰸡�
��1��
�⣺��С�����˶���B����ٶ�ΪvB���ɻ�е���غ㶨���У�mgR= ![]() mvB2����
mvB2����
�������ݽ�ã�vB=3 ![]() m/s
m/s
��ţ�ٵڶ������У�F��mg=m ![]() ����
����
�����٢ڽ��С������B������֧���� F=30N����
��ţ�ٵ��������У�С������B��ʱ��Բ����ѹ��Ϊ30N����
��2��
�⣺��С�����˶���C����ٶ�ΪvC���ɶ��ܶ���mgR��mgL= ![]() mvC2 ����
mvC2 ����
���С������C����ٶ� vC=4m/s����
С����ƽ�������ˮƽ����S=vCt=vC ![]() =1.2m����
=1.2m����
��d=hcot��=0.78m����
��ΪS��d������С�����뿪C����䵽б���ϡ���
��ˣ�С�����C���˶������������ʱ�伴ΪС����ƽ���˶�����ʱ��Ϊ��
t= ![]() =0.3s
=0.3s
����������1����������Բ���˶�����е���غ㣬�ɻ�е���غ㶨�ɿɵó�����B����ٶȣ�������������ʽ�����С���Բ����ѹ������2����B��C�������ȼ����˶��������ɶ��ܶ���������˶��������C����ٶȣ�С���뿪C����ƽ���˶�������ƽ���˶��ܷ��䵽б���ϣ���������б����������ֱ���˶����ʱ�䣬���䵽б���ϣ���Ҫ�ֶο��ǣ�
�����㾫���������������Ͷ��ܶ������ۺ�Ӧ�ö���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪����������ָ��Բ�ģ��������ļ��ٶȣ�������ֻ�ı����ٶȵķ����ı��ٶȵĴ�С���������Ǹ�������Ч��������.�ڷ�����Բ���˶����ʵ��������ʱ��ǧ������������֮��������һ����������Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݣ�

 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
��ͨ����ͬ����ϰ��ϵ�д�