题目内容
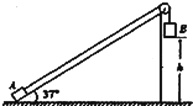
【题目】如图所示,长L=2.9m,倾角![]() 的斜面固定在水平面上,斜面顶端固定一个不计摩擦的轻滑轮。质量为m的木块A和质量为M的铁块B用一根轻绳相连,M=3m。开始时,木块A锁定在斜面底端,铁块B通过滑轮悬挂在离地h=1.6m的空中,木块A和铁块B均可视为质点。若木块A与斜面的动摩擦因数
的斜面固定在水平面上,斜面顶端固定一个不计摩擦的轻滑轮。质量为m的木块A和质量为M的铁块B用一根轻绳相连,M=3m。开始时,木块A锁定在斜面底端,铁块B通过滑轮悬挂在离地h=1.6m的空中,木块A和铁块B均可视为质点。若木块A与斜面的动摩擦因数![]() =0.5,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8。将木块A解除锁定后,试求:
=0.5,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8。将木块A解除锁定后,试求:
(1)落地前铁块B加速度的大小。
(2)木块A沿斜面上滑的最大速度。
(3)若M=km(k为正整数),要使木块A 能到达斜面顶端,k至少多大?
【答案】(1)5m/s2. (2)4m/s. (3)10.
【解析】(1)设铁块落地之前加速度大小为![]() ,绳子拉力为
,绳子拉力为![]() ,则
,则
对B: ![]()
对A: ![]() 联立并代入数据得:
联立并代入数据得: ![]()
(2)铁块落地瞬间,木块沿斜面上滑的速度最大,设为![]()
由![]() 代入数据得:
代入数据得: ![]()
(3)若![]() ,设铁块落地之前加速度大小为
,设铁块落地之前加速度大小为![]() ,绳子拉力为
,绳子拉力为![]() ,则:
,则:
对B![]()
对A: ![]()
解得: ![]()
设铁块落地后,木块沿斜面减速上滑的加速度为![]() :
:
![]()
解得: ![]() (负号表示与运动方向相反)
(负号表示与运动方向相反)
木块恰冲到斜面顶端时末速度为0,设铁块落地瞬间木块的速度为![]() ,则:
,则:
![]()
![]()
联立解得: ![]() 由题意知,k至少取10;
由题意知,k至少取10;
综上所述本题答案是:(1)5m/s2. (2)4m/s. (3)10.

练习册系列答案
相关题目