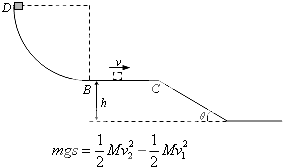��Ŀ����
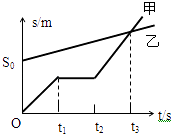
����Ŀ��һ���ʹ�װ����ͼ��ʾ������AB����ˮƽ�ģ�����LAB=4m��BC������б�ģ�����lBC=5m�����Ϊ��=37�㣬AB��BC��B��ͨ��һ�μ��̵�Բ�����ӣ�ͼ��δ����Բ���������ʹ���v=4m/s�ĺ㶨����˳ʱ����ת����֪�����봫�ʹ���Ķ�Ħ��������=0.5���������ٶ�gȡ10m/s2 �� �ֽ�һ���������ɿ����ʵ㣩���ٶȵط���A�㣬��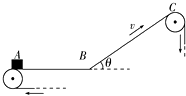
��1��������һ�ε���B�����õ�ʱ�䣿
��2�������ش��ʹ����������߶ȣ�
��3�������˶���23sʱ���ڵ�λ�ã�
���𰸡�
��1��
�⣺�����շ���ˮƽ���ʹ��ϵļ��ٶ�Ϊa1
��ţ�ٵڶ����ɵæ�mg=ma1
���a1=��g=5 m/s2
��t1ʱ���봫�ʹ����ٶ���ͬ����t1= ![]() =0.8 s
=0.8 s
ǰ����λ��Ϊx1= ![]() a1t12=1.6 m
a1t12=1.6 m
�˺����봫�ʹ�һ�������˶���B�㣬��ʱt2= ![]() =0.6 s
=0.6 s
���Թ�����һ�ε���B�����õ�ʱ��t=t1+t2=1.4 s
��2��
�⣺�蹤�����������߶�Ϊh���ɶ��ܶ�����
����mgcos �ȩ�mgsin �ȣ� ![]() =0��
=0�� ![]() mv2
mv2
���h=2.4 m
��3��
�⣺�����ش��ʹ������˶���ʱ��Ϊt3= ![]() =2 s
=2 s
�˺����ڹ����ڴ��ʹ�����б���˶�ʱ�ļ��ٶ���ͬ���ڴ��ʹ���ˮƽ���˶�ʱ�ļ��ٶ�Ҳ��ͬ���ʹ������ڴ��ʹ����������˶���������ΪT
T=2t1+2t3=5.6 s
�����ӿ�ʼ�˶�����һ�η��ش��ʹ���ˮƽ���֣����ٶȱ�Ϊ������ʱ��
t0=2t1+t2+2t3=6.2 s
��23 s=t0+3T
��˵����23 s����ǡ���˶������ʹ���ˮƽ���֣����ٶ�Ϊ�㣮
�ʹ�����A���Ҳ࣬��A��ľ���x=LAB��x1=2.4 m
�������������շ���ˮƽ���ʹ��Ͻ�����������������ţ�ٵڶ����ɺ��˶�ѧ��ʽ������⣮�ɶ��ܶ����������������߶ȣ����ڹ����ڴ��ʹ�����б���˶�ʱ�ļ��ٶ���ͬ���ڴ��ʹ���ˮƽ���˶�ʱ�ļ��ٶ�Ҳ��ͬ���ʹ������ڴ��ʹ����������˶����ҳ����������ʱ��Ĺ�ϵ��
�����㾫����������Ŀ����֪���������ö��ܶ������ۺ�Ӧ�õ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ����Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݣ�