题目内容
12. 如图所示,一个矩形线圈的ab、cd边长L1=$\sqrt{2}m$,ad,bc边长L2=1m,线圈匝数N=100匝,线圈处于磁感应强度B=0.01T的水平匀强磁场中,并以OO′为轴做匀速转动(OO′与磁场方向垂直,线圈电阻不计),线圈转动的角速度ω=10rad/s,现将该线圈输出端通过变比为k=2的理想变压器(原副线圈匝数之比为2:1)与电阻为R=1Ω的电动机相连,同时用此电动机将竖直固定的光滑U型金属框架上的水平导体棒EF从静止向上拉起(不计电动机的摩擦损耗),测得矩形线圈中形成的电流有效值为I=1A.已知导体棒的质量m=0.5kg,U型金属框架宽L=$\sqrt{5}$m且足够长,空间存在垂直框架平面磁感应强度B0=1T的匀强磁场,当导体棒上升的时间t0>1s时其速度恰好稳定,棒有效电阻R0=4Ω,金属框架的总电阻r0=1Ω并认为不变.棒与金属框架接触良好,重力加速度g=10m/s2,求:
如图所示,一个矩形线圈的ab、cd边长L1=$\sqrt{2}m$,ad,bc边长L2=1m,线圈匝数N=100匝,线圈处于磁感应强度B=0.01T的水平匀强磁场中,并以OO′为轴做匀速转动(OO′与磁场方向垂直,线圈电阻不计),线圈转动的角速度ω=10rad/s,现将该线圈输出端通过变比为k=2的理想变压器(原副线圈匝数之比为2:1)与电阻为R=1Ω的电动机相连,同时用此电动机将竖直固定的光滑U型金属框架上的水平导体棒EF从静止向上拉起(不计电动机的摩擦损耗),测得矩形线圈中形成的电流有效值为I=1A.已知导体棒的质量m=0.5kg,U型金属框架宽L=$\sqrt{5}$m且足够长,空间存在垂直框架平面磁感应强度B0=1T的匀强磁场,当导体棒上升的时间t0>1s时其速度恰好稳定,棒有效电阻R0=4Ω,金属框架的总电阻r0=1Ω并认为不变.棒与金属框架接触良好,重力加速度g=10m/s2,求:(1)导体棒匀速上升时的速度;
(2)若0~1s时间内导体棒产生的焦耳热Q=0.75J,并已知1s时间内上升高度为h=1m,求1s时刻导体棒的速度.
(3)若竖直光滑U型金属框架不固定地靠在竖直墙壁上,其下端置于水平地面上,金属框架质量M=1kg,问当矩形线圈转动的角速度ω取何值时,被拉导棒速度稳定后矩形线圈中的电流I0=2A,且竖直光滑U型金属框架与水平地面间作用力刚好为零?
分析 (1)由交流电产生的原理求出线圈中产生的最大电动势及其有效值,然后由又变压器的关系公式求出电动机两端的电压与电动机的输出功率;最后结合导体棒切割磁感线的功能转化关系,即可求出导体棒匀速上升时的速度;
(2)导体棒向上运动的过程中,电动机做的功转化为棒的动能、棒的势能以及线框与棒中产生的内能,由此即可求出棒的速度;
(3)对导体框进行受力分析,求出导体框受到的安培力,由F=BIL求出线框中的电流,由闭合电路的欧姆定律求出棒中的电动势,由E=BLv求出棒的速度,由P=Fv求出电动机的输出功率,最后结合变压器的匝数比以及交流电的产生,求出矩形线圈转动的角速度ω.
解答 解:(1)线圈在转动的过程中产生的最大电动势:${E}_{m1}=NB{L}_{1}{L}_{2}ω=100×0.01×\sqrt{2}×1×10=10\sqrt{2}$V
线圈中的电动势的有效值:${E}_{1}=\frac{{E}_{m1}}{\sqrt{2}}=10$V
线圈输出的功率:P1=E1I1=10×1=10W
电动机上的电压:${U}_{1}=\frac{{E}_{1}}{k}=\frac{10}{2}=5$V
电动机上的电流:${I}_{1}′=\frac{{P}_{1}}{{U}_{1}}=\frac{10}{5}=2$A
电动机的输出功率:${P}_{出}={P}_{1}-I{′}_{1}^{2}R=10-{2}^{2}×1=6$W
当导体棒向上的匀速运动的过程中,产生的电动势:E2=B0Lv1
感应电流:${I}_{2}=\frac{{E}_{2}}{{R}_{0}+{r}_{0}}$
导体棒受到的安培力:${F}_{1}={B}_{0}{I}_{2}L=\frac{{B}_{0}^{2}{L}^{2}{v}_{1}}{{R}_{0}+{r}_{0}}$
导体棒做匀速运动,绳子的拉力等于重力与安培力的和,即:F=F1+mg
绳子拉力的功率等于电动机的输出的功率,即:P出=Fv1
联立得:v1=1m/s
(2)若0~1s时间内导体棒产生的焦耳热Q=0.75J,由于导体棒与线框中的电流是相等的,由:Q=I2Rt可得:
$Q′=\frac{{r}_{0}}{{R}_{0}}Q=\frac{1}{4}×0.75=0.1875$J
导体棒向上运动的过程中,电动机做的功转化为棒的动能、棒的势能以及线框与棒中产生的内能.即:
${P}_{出}t=mgh+\frac{1}{2}m{v}_{2}^{2}+Q+Q′$
代入数据得:v2=0.5m/s
(3)竖直光滑U型金属框架与水平地面间作用力刚好为零时,框架的下边受到的安培力:
B0I3L=Mg
电路中产生的电动势:E3=B0Lv3
所以电路中的电流:${I}_{3}=\frac{{E}_{3}}{{R}_{0}+{r}_{0}}$
所以:${v}_{3}=\frac{Mg({R}_{0}+{r}_{0})}{{B}_{0}^{2}{L}^{2}}=\frac{1×10×(4+1)}{{1}^{2}×(\sqrt{5})^{2}}=10$m/s
EF达到稳定时,受到的拉力等于受到的安培力与重力的和,即:F′=mg+B0I3L
代入数据得:F′=15N
所以拉力的功率,即电动机的输出功率:P出′=F′v3=15×10=150W
此时矩形线圈中的电流I0=2A,则流过电动机的电流:I4=kI0=2×2=4A
电动机的输入功率:${P}_{2}′={I}_{4}^{2}R+{P}_{出}′={4}^{2}×1+150=166$W
由于电动机的输入功率等于矩形线圈的输出功率,所以矩形线圈的输出功率为:P2=166W,
又:P2=E0•I0
则:${E}_{0}=\frac{{P}_{2}}{{I}_{0}}=\frac{166}{2}=84$V
该电动势是有效电动势,则最大电动势:${E}_{2m}=\sqrt{2}{E}_{2}$
又:E2m=NBL1L2ω′
所以:$ω′=\frac{{E}_{2m}}{NB{L}_{1}{L}_{2}}=\frac{84\sqrt{2}}{100×0.01×1×\sqrt{2}}=84$rad/s
答:(1)导体棒匀速上升时的速度1m/s;
(2)若0~1s时间内导体棒产生的焦耳热Q=0.75J,并已知1s时间内上升高度为h=1m,1s时刻导体棒的速度是0.5m/s.
(3)当矩形线圈转动的角速度ω取 84rad/s时,竖直光滑U型金属框架与水平地面间作用力刚好为零.
点评 该题将恒定电流与闭合电路的欧姆定律、电磁感应定律的综合应用、交流电的有效值与最大值结合在一起,涉及到的知识点多,物理过程多,物理量多、公式多、属于难度变态的题目,做这一类的题目要有足够的耐心与信心.

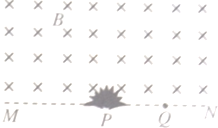 如图所示,在直线MN上方存在着垂直于纸面向里的匀强磁场,放置直线MN上P点的粒子源(粒子均带负电),可以向磁场区域纸面内的各个方向发射出比荷k和速率v均相同的粒子,PQ间距离等于粒子的轨道半径R,则过Q点的离子的运动时间为( )
如图所示,在直线MN上方存在着垂直于纸面向里的匀强磁场,放置直线MN上P点的粒子源(粒子均带负电),可以向磁场区域纸面内的各个方向发射出比荷k和速率v均相同的粒子,PQ间距离等于粒子的轨道半径R,则过Q点的离子的运动时间为( )| A. | $\frac{2πR}{v}$ | B. | $\frac{πR}{3v}$ | C. | $\frac{5πR}{3v}$ | D. | $\frac{πR}{v}$ |
①已知灵敏电流计G的满偏电流Ig=100μA、内阻rg=2.0kΩ,若要改装后的电流表满偏电流为200mA,应并联一只1.0Ω(保留一位小数)的定值电阻R1;
②根据图甲,用笔画线代替导线将图乙连接成完整电路;
③某次试验的数据如表所示:该小组借鉴“研究匀变速直线运动”试验中计算加速度的方法(逐差法),计算出电池组的内阻r=1.66Ω(保留两位小数);为减小偶然误差,逐差法在数据处理方面体现出的主要优点是充分利用已获得的数据.
| 测量次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 电压表V读数U/V | 5.26 | 5.16 | 5.04 | 4.94 | 4.83 | 4.71 | 4.59 | 4.46 |
| 改装表A读数I/mA | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |

 如图,某同学在一次实验测试中,利用弹簧枪将质量为m的钢珠以某一初速度从A点水平射出,发现钢珠能够恰好从弯曲圆管BCD的B点无撞击地进入圆弧,最终从圆管的最高点D射出后落到斜面上的E点,已知两圆弧的半径为均R,且A与D在同一水平线上,图中角θ=60°,斜面上O′到E点距离也为R,求
如图,某同学在一次实验测试中,利用弹簧枪将质量为m的钢珠以某一初速度从A点水平射出,发现钢珠能够恰好从弯曲圆管BCD的B点无撞击地进入圆弧,最终从圆管的最高点D射出后落到斜面上的E点,已知两圆弧的半径为均R,且A与D在同一水平线上,图中角θ=60°,斜面上O′到E点距离也为R,求 如图所示,一个质量为m,电荷量为q的正离子,在D处沿图示方向以一定的速度射入磁感应强度为B的匀强磁场中,此磁场方向是垂直纸面向里.结果离子正好从距A点为d的小孔C沿垂直于电场方向进入匀强电场,此电场方向与AC平行且向上,最后离子打在G处,而G处距A点4d(AG⊥AC).不计离子重力,离子运动轨迹在纸面内.求:
如图所示,一个质量为m,电荷量为q的正离子,在D处沿图示方向以一定的速度射入磁感应强度为B的匀强磁场中,此磁场方向是垂直纸面向里.结果离子正好从距A点为d的小孔C沿垂直于电场方向进入匀强电场,此电场方向与AC平行且向上,最后离子打在G处,而G处距A点4d(AG⊥AC).不计离子重力,离子运动轨迹在纸面内.求: 测量小物块0与平板P之间动摩擦因数的实验装置如图所示.是半径足够大的、光滑的四分之一圆弧轨道,与水平固定放置的P板的上表面BC在B点相切,C点在水平地 面的垂直投影为C′.重力加速度大小为g.实验步骤如下:
测量小物块0与平板P之间动摩擦因数的实验装置如图所示.是半径足够大的、光滑的四分之一圆弧轨道,与水平固定放置的P板的上表面BC在B点相切,C点在水平地 面的垂直投影为C′.重力加速度大小为g.实验步骤如下:
 在同一水平面中的光滑平行导轨P、Q相距L=1m,导轨左端接有如图所示的电路.其中水平放置的平行板电容器两极板M、N间距离d=10mm,定值电阻R1=R2=12Ω,R3=2Ω,金属棒ab电阻r=2Ω,其它电阻不计.磁感应强度B=1T的匀强磁场竖直穿过导轨平面,当金属棒ab沿导轨向右匀速运动时,悬浮于电容器两极板之间,质量m=1×10-14kg,带电量q=-1×10-14C的微粒恰好静止不动.取g=10m/s2,在整个运动过程中金属棒与导轨接触良好.且运动速度保持恒定.试求:
在同一水平面中的光滑平行导轨P、Q相距L=1m,导轨左端接有如图所示的电路.其中水平放置的平行板电容器两极板M、N间距离d=10mm,定值电阻R1=R2=12Ω,R3=2Ω,金属棒ab电阻r=2Ω,其它电阻不计.磁感应强度B=1T的匀强磁场竖直穿过导轨平面,当金属棒ab沿导轨向右匀速运动时,悬浮于电容器两极板之间,质量m=1×10-14kg,带电量q=-1×10-14C的微粒恰好静止不动.取g=10m/s2,在整个运动过程中金属棒与导轨接触良好.且运动速度保持恒定.试求: