题目内容
4.某同学利用如图1所示的装置测量当地的重力加速度,实验步骤如下:A.按装置图安装好实验装置
B.用游标卡尺测量小球的直径d
C.用米尺测量悬线的长度l
D.让小球在竖直平面内小角度摆动.当小球经过最低点时开始计时,并计数为0,此后小球每经过最低点一次,依次计数1、2、3、…当数到20时,停止计时,测得时间为t
E.多次改变悬线长度,对应每个悬线长度,都重复实验步骤C、D
F.计算出每个悬线长度对应的t2
G.以t2为纵坐标、l为横坐标,作出t2-l图线

(1)用游标卡尺测量小球的直径.某次测量的示数如图2所示读出小球直径d的值为1.52cm.
(2)该同学利用计算机作出图线如图3所示.根据图线拟合得到方程t2=404.0l+3.5.由此可以得出当地的重力加速度g=9.76m/s2.(取π2=9.86,结果保留3位有效数字)
(3)从理论上分析图线没有过坐标原点的原因,下列分析正确的是
A.不应在小球经过最低点时开始计时,应该在小球运动到最高点时开始计时
B.开始计时后,不应记录小球经过最低点的次数,而应记录小球做全振动的次数
C.不应作t2-l图线,而应作t2-(l-$\frac{1}{2}$d)图线
D.不应作t2-l图线,而应作t2-(l+$\frac{1}{2}$d)图线.
分析 (1)游标卡尺主尺与游标尺示数之和是游标卡尺的示数.
(2)根据单摆周期公式求出t2-l函数关系式,然后求出重力加速度.
(3)单摆摆长等于摆线长度与摆球半径之和,以摆线长度作为摆长,则摆长偏小.
解答 解:(1)由图示游标卡尺可知,主尺示数是1.5cm,游标尺示数是2×0.1mm=0.2mm=0.02cm,
游标卡尺示数即小球的直径d=1.5cm+0.02cm=1.52cm;
(2)由题意知,单摆的周期T=$\frac{t}{\frac{n}{2}}$=$\frac{t}{10}$,
由单摆周期公式T=2π$\sqrt{\frac{l}{g}}$可得:t2=$\frac{400{π}^{2}}{g}$l,
由图象得到的方程为:t2=404.0l+3.5,
则$\frac{400{π}^{2}}{g}$=404.0,g=$\frac{400{π}^{2}}{404}$≈9.76m/s2;
(3)单摆摆长等于摆线长度与摆球半径之和,把摆线长度作为单摆摆长,
摆长小于实际摆长,t2-l图象不过原点,在纵轴上截距不为零,故D正确,ABC错误;
故答案为:(1)1.52;(2)9.76;(3)D.
点评 游标卡尺主尺与游标尺示数之和是游标卡尺示数,对游标卡尺读数时,要确定游标尺的精度,游标尺是10分度的,精度为0.1mm,游标尺是20分度的,精度是0.05mm,游标尺是50分度的,精度为0,02mm;同时掌握单摆周期公式T=2π$\sqrt{\frac{l}{g}}$的应用,注意t2-l图象不过原点的原因.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19. 如图中带箭头的实线表示某个电场的电场线,实线间距相等且相互平行,一个带电离子从P处飞入这个电场(如图所示),以下说法中正确的是( )
如图中带箭头的实线表示某个电场的电场线,实线间距相等且相互平行,一个带电离子从P处飞入这个电场(如图所示),以下说法中正确的是( )
 如图中带箭头的实线表示某个电场的电场线,实线间距相等且相互平行,一个带电离子从P处飞入这个电场(如图所示),以下说法中正确的是( )
如图中带箭头的实线表示某个电场的电场线,实线间距相等且相互平行,一个带电离子从P处飞入这个电场(如图所示),以下说法中正确的是( )| A. | 离子受的电场力方向一定向右 | B. | 离子受的电场力大小、方向都不变 | ||
| C. | 离子电势能肯定减少 | D. | 离子一定做匀变速运动 |
16.下列说法正确的有( )
| A. | 氡的半衰期为3.8天,1克氡经过7.6天后还剩0.25克氡未衰变 | |
| B. | 原子核内的中子转化成一个质子和一个电子,这种转化产生的电子发射到核外,就是β粒子,这就是β衰变的实质 | |
| C. | 某种材料的逸出功是W,则它的极限频率为γ0=$\frac{W}{h}$ | |
| D. | 只要有核反应发生,就一定会释放出核能 | |
| E. | 一个处于n=3能级的氢原子自发跃迁时,能发出3种频率的光子 |
13.质量为3m的机车,其速度为v0,在与质量为2m的静止车厢碰撞后挂接在一起运动,其运动速度应为( )
| A. | $\frac{{2{V_0}}}{5}$ | B. | $\frac{{3{V_0}}}{5}$ | C. | $\frac{{2{V_0}}}{3}$ | D. | $\frac{{3{V_0}}}{2}$ |

 如图所示,某人乘雪橇从雪坡经A点滑到B点,接着沿水平路面滑至C点停止.人与雪橇的总质量为70kg.开始时人与雪橇距水平路面的高度h=20m,经A、B两点时的速度分别是2m/s和12m/s,g取10m/s2,试求:
如图所示,某人乘雪橇从雪坡经A点滑到B点,接着沿水平路面滑至C点停止.人与雪橇的总质量为70kg.开始时人与雪橇距水平路面的高度h=20m,经A、B两点时的速度分别是2m/s和12m/s,g取10m/s2,试求: 如图所示,一个矩形线圈的ab、cd边长L1=$\sqrt{2}m$,ad,bc边长L2=1m,线圈匝数N=100匝,线圈处于磁感应强度B=0.01T的水平匀强磁场中,并以OO′为轴做匀速转动(OO′与磁场方向垂直,线圈电阻不计),线圈转动的角速度ω=10rad/s,现将该线圈输出端通过变比为k=2的理想变压器(原副线圈匝数之比为2:1)与电阻为R=1Ω的电动机相连,同时用此电动机将竖直固定的光滑U型金属框架上的水平导体棒EF从静止向上拉起(不计电动机的摩擦损耗),测得矩形线圈中形成的电流有效值为I=1A.已知导体棒的质量m=0.5kg,U型金属框架宽L=$\sqrt{5}$m且足够长,空间存在垂直框架平面磁感应强度B0=1T的匀强磁场,当导体棒上升的时间t0>1s时其速度恰好稳定,棒有效电阻R0=4Ω,金属框架的总电阻r0=1Ω并认为不变.棒与金属框架接触良好,重力加速度g=10m/s2,求:
如图所示,一个矩形线圈的ab、cd边长L1=$\sqrt{2}m$,ad,bc边长L2=1m,线圈匝数N=100匝,线圈处于磁感应强度B=0.01T的水平匀强磁场中,并以OO′为轴做匀速转动(OO′与磁场方向垂直,线圈电阻不计),线圈转动的角速度ω=10rad/s,现将该线圈输出端通过变比为k=2的理想变压器(原副线圈匝数之比为2:1)与电阻为R=1Ω的电动机相连,同时用此电动机将竖直固定的光滑U型金属框架上的水平导体棒EF从静止向上拉起(不计电动机的摩擦损耗),测得矩形线圈中形成的电流有效值为I=1A.已知导体棒的质量m=0.5kg,U型金属框架宽L=$\sqrt{5}$m且足够长,空间存在垂直框架平面磁感应强度B0=1T的匀强磁场,当导体棒上升的时间t0>1s时其速度恰好稳定,棒有效电阻R0=4Ω,金属框架的总电阻r0=1Ω并认为不变.棒与金属框架接触良好,重力加速度g=10m/s2,求: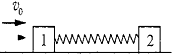 光滑水平面上静置两个小木块1和2,其质量分别为m1=1.0kg、m2=4.0kg,它们中间用一根轻质弹簧相连.一颗水平飞行的子弹质量为m=50.0g,以v0=500m/s的速度在极短时间内射穿两木块,已知射穿木块1后子弹的速度变为原来的$\frac{3}{5}$,且子弹损失的动能为射穿木块2损失动能的2倍.求系统运动过程中弹簧的最大弹性势能.
光滑水平面上静置两个小木块1和2,其质量分别为m1=1.0kg、m2=4.0kg,它们中间用一根轻质弹簧相连.一颗水平飞行的子弹质量为m=50.0g,以v0=500m/s的速度在极短时间内射穿两木块,已知射穿木块1后子弹的速度变为原来的$\frac{3}{5}$,且子弹损失的动能为射穿木块2损失动能的2倍.求系统运动过程中弹簧的最大弹性势能.