题目内容
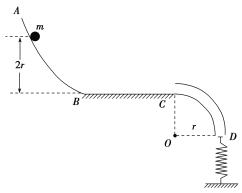
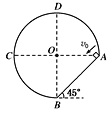
【题目】如图所示,由倾角为45°的粗糙斜面AB和半径为0.5 m的![]() 光滑圆弧组成的轨道固定在竖直平面内,斜面和圆弧之间由小圆弧(长度不计)平滑连接,其中B为最低点,D为最高点,C、A两点和圆弧圆心O在同一水平线上.一物块(可视为质点)在A点以初速度v0=
光滑圆弧组成的轨道固定在竖直平面内,斜面和圆弧之间由小圆弧(长度不计)平滑连接,其中B为最低点,D为最高点,C、A两点和圆弧圆心O在同一水平线上.一物块(可视为质点)在A点以初速度v0=![]() m/s沿斜面向下沿内轨道运动.物块与斜面间的动摩擦因数为μ,取重力加速度大小g=10 m/s2,则下列说法正确的是( )
m/s沿斜面向下沿内轨道运动.物块与斜面间的动摩擦因数为μ,取重力加速度大小g=10 m/s2,则下列说法正确的是( )
A. 若μ值满足一定的条件,则物块可能从D处开始做自由落体运动
B. 若μ值满足一定的条件,则物块可能最终从AD圆弧某处脱离轨道
C. 若μ=0.2,则物块最终从CD圆弧某处脱离轨道
D. 若μ=0.6,则物块始终不会脱离轨道
【答案】CD
【解析】
物体恰好能够达到D点时的条件为![]() ,根据物体运动情况和受力情况进行分析,判断最终物体离开轨道的位置;
,根据物体运动情况和受力情况进行分析,判断最终物体离开轨道的位置;
A、若物块能够达到D点,则在D点的速度不可能为零,所以物块不可能从D处开始做自由落体运动,故A错误;
B、若物块能够通过D点,则一定能够从AD圆弧沿轨道向下运动,不会从AD脱离轨道,故B错误;
C、物体恰好能够达到D点时,则![]() ,解得
,解得![]() ;
;
若![]() ,设物体在AB轨道通过n次后达到D点速度刚好为
,设物体在AB轨道通过n次后达到D点速度刚好为![]() ,则根据动能定理可得:
,则根据动能定理可得:![]() ,
,
解得:![]() 次,所以物体通过AB第二次以后将不能达到D点,会从CD圆弧某处脱离轨道,做斜上抛运动;若
次,所以物体通过AB第二次以后将不能达到D点,会从CD圆弧某处脱离轨道,做斜上抛运动;若![]() ,代入可以得到
,代入可以得到![]() ,说明不会通过最高点,物块始终不会脱离轨道,故选项CD正确。
,说明不会通过最高点,物块始终不会脱离轨道,故选项CD正确。

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目