题目内容
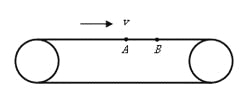
【题目】如图，光滑水平直轨道上有三个质量均为m的物块A、B、C。 B的左侧固定一轻弹簧（弹簧左侧的挡板质量不计).设A以速度ｖ0朝B运动，压缩弹簧；当A、 B速度相等时，B与C恰好相碰并粘接在一起，然后继续运动。假设B和C碰撞过程时间极短。求从Ａ开始压缩弹簧直至与弹簧分离的过程中，求：
（1）碰撞过程中C物块受到的冲量大小；
（2）B、C碰撞前弹簧压缩到最短时的弹性势能与B、C碰撞后弹簧压缩到最短时的弹性势能之比；
【答案】（1）
（2）
【解析】
根据动量守恒定律和能量守恒定律联立即可求出碰撞过程中C物块受到的冲量大小；系统动量守恒，由动量守恒定律求出速度，然后应用能量守恒定律可以求出弹簧的弹性势能。
（1）从A压缩弹簧到A与B具有相同速度v1时，对A、B与弹簧组成的系统，根据动量守恒定律得：
B与C发生完全非弹性碰撞时，设碰撞后的瞬时速度为v2，对B、C组成的系统，由动量守恒和能量守恒定律得：
B与C发生完全非弹性碰撞过程中，对C根据动量定理：I=mv2-0
联立可得：
（2）B、C碰撞前弹簧压缩到最短时，根据能量守恒，此时的弹性势能：
可得：
B、C碰撞后瞬间至弹簧压缩到最短的过程中，根据动量守恒：
B、C碰撞后瞬间至弹簧压缩到最短的过程中，根据能量守恒：
联立可得：
则有：
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
