题目内容
3.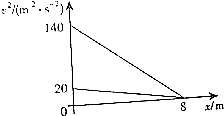 某物体以一定初速度从斜面底端冲上斜面,到达最高点后,再返回到斜面底端,此过程以斜面底端作为位移起点,取沿斜面向上为位移正方向,物体的速度的平方与位移的函数关系如图所示,由v2-x图象可知( )
某物体以一定初速度从斜面底端冲上斜面,到达最高点后,再返回到斜面底端,此过程以斜面底端作为位移起点,取沿斜面向上为位移正方向,物体的速度的平方与位移的函数关系如图所示,由v2-x图象可知( )| A. | 斜面倾角为30° | |
| B. | 斜面倾角为60° | |
| C. | 物体与斜面间的动摩擦因数约为0.87 | |
| D. | 物体与斜面间的动摩擦因数约为0.43 |
分析 在上滑过程和下滑过程分别利用动能定理即可求得斜面倾角和摩擦因数
解答 解:在上滑过程中,由动能定理可得:
$-mgxsinθ-μmgxcosθ=0-\frac{1}{2}m{v}^{2}$
在下滑过程中由动能定理可得:
$mgxsinθ-μmgxcosθ=\frac{1}{2}m{v′}^{2}-0$
联立解得:θ=30°,μ=,0.43
故选:AD
点评 本题主要考查了动能定理,抓住上滑过程和下滑过程,不能作为整个过程利用动能定理

练习册系列答案
相关题目
20.下列有关科学家和其在物理学中的贡献描述正确的是( )
| A. | 卡文迪什发现了万有引力定律 | B. | 法拉第发现了电流的磁效应 | ||
| C. | 贝克勒尔首先发现了天然放射现象 | D. | 汤姆生提出了原子的核式结构模型 |
1. 如图所示,将面积为S,电阻为R的线框abcd水平置于地面上某处(ab边朝北方,cd边朝南方),如果将其从图示位置翻转放置,测得通过线框的电荷量为Q1,如果将其从图示位置以cd边为轴竖立起来,这过程中测得通过线框的电荷量为Q2,则该处地磁场的磁感应强度大小为( )
如图所示,将面积为S,电阻为R的线框abcd水平置于地面上某处(ab边朝北方,cd边朝南方),如果将其从图示位置翻转放置,测得通过线框的电荷量为Q1,如果将其从图示位置以cd边为轴竖立起来,这过程中测得通过线框的电荷量为Q2,则该处地磁场的磁感应强度大小为( )
 如图所示,将面积为S,电阻为R的线框abcd水平置于地面上某处(ab边朝北方,cd边朝南方),如果将其从图示位置翻转放置,测得通过线框的电荷量为Q1,如果将其从图示位置以cd边为轴竖立起来,这过程中测得通过线框的电荷量为Q2,则该处地磁场的磁感应强度大小为( )
如图所示,将面积为S,电阻为R的线框abcd水平置于地面上某处(ab边朝北方,cd边朝南方),如果将其从图示位置翻转放置,测得通过线框的电荷量为Q1,如果将其从图示位置以cd边为轴竖立起来,这过程中测得通过线框的电荷量为Q2,则该处地磁场的磁感应强度大小为( )| A. | B=$\frac{R}{S}$$\sqrt{\frac{1}{4}{{Q}_{1}}^{2}+{{Q}_{2}}^{2}}$ | B. | B=$\frac{R}{S}$$\sqrt{{{Q}_{1}}^{2}+{{Q}_{2}}^{2}}$ | ||
| C. | B=$\frac{R}{S}$$\sqrt{\frac{1}{2}{{Q}_{1}}^{2}+{Q}_{1}{Q}_{2}+{{Q}_{2}}^{2}}$ | D. | B=$\frac{R}{S}$$\sqrt{{{Q}_{1}}^{2}+{Q}_{1}{Q}_{2}+{{Q}_{2}}^{2}}$ |
18. 如图所示装置,密度相同、大小不同的球状纳米颗粒在电离室中电离后带正电,电量与其表面积成之比,电离后,颗粒缓慢通过小孔O1进入极板间电压为U的水平加速电场区域I,再通过小孔O2射入电场强度为E的匀强电场区域Ⅱ,区域Ⅱ中极板长度为l,极板间距为d,假设不计颗粒重力,且所有颗粒均能从区域Ⅱ右侧离开,则( )
如图所示装置,密度相同、大小不同的球状纳米颗粒在电离室中电离后带正电,电量与其表面积成之比,电离后,颗粒缓慢通过小孔O1进入极板间电压为U的水平加速电场区域I,再通过小孔O2射入电场强度为E的匀强电场区域Ⅱ,区域Ⅱ中极板长度为l,极板间距为d,假设不计颗粒重力,且所有颗粒均能从区域Ⅱ右侧离开,则( )
 如图所示装置,密度相同、大小不同的球状纳米颗粒在电离室中电离后带正电,电量与其表面积成之比,电离后,颗粒缓慢通过小孔O1进入极板间电压为U的水平加速电场区域I,再通过小孔O2射入电场强度为E的匀强电场区域Ⅱ,区域Ⅱ中极板长度为l,极板间距为d,假设不计颗粒重力,且所有颗粒均能从区域Ⅱ右侧离开,则( )
如图所示装置,密度相同、大小不同的球状纳米颗粒在电离室中电离后带正电,电量与其表面积成之比,电离后,颗粒缓慢通过小孔O1进入极板间电压为U的水平加速电场区域I,再通过小孔O2射入电场强度为E的匀强电场区域Ⅱ,区域Ⅱ中极板长度为l,极板间距为d,假设不计颗粒重力,且所有颗粒均能从区域Ⅱ右侧离开,则( )| A. | 颗粒的比荷与半径成正比 | |
| B. | 所有的颗粒从同一位置离开区域Ⅱ | |
| C. | 所有的颗粒在区域Ⅱ中运动时间相同 | |
| D. | 半径越大的颗粒离开区域Ⅱ时动能越大 |
8.若风吹到风车叶片上的动能全部转化成风车能量,当风速度为v时风车获得的功率为P,若风速度提高到2v时风车获得的功率为( )
| A. | 2P | B. | 4P | C. | 8P | D. | 16P |
13. 两根长度分别为l和$\frac{l}{2}$细长轻绳下端拴质量相等的小球构成单摆,两悬点在同一竖直线上且间距为$\frac{l}{2}$,现将单摆向左拉开一个小角度,然后无初速地释放,若小球碰撞时无能量损失,小球可视为质点,对于以后的运动,下列说法中正确的是( )
两根长度分别为l和$\frac{l}{2}$细长轻绳下端拴质量相等的小球构成单摆,两悬点在同一竖直线上且间距为$\frac{l}{2}$,现将单摆向左拉开一个小角度,然后无初速地释放,若小球碰撞时无能量损失,小球可视为质点,对于以后的运动,下列说法中正确的是( )
 两根长度分别为l和$\frac{l}{2}$细长轻绳下端拴质量相等的小球构成单摆,两悬点在同一竖直线上且间距为$\frac{l}{2}$,现将单摆向左拉开一个小角度,然后无初速地释放,若小球碰撞时无能量损失,小球可视为质点,对于以后的运动,下列说法中正确的是( )
两根长度分别为l和$\frac{l}{2}$细长轻绳下端拴质量相等的小球构成单摆,两悬点在同一竖直线上且间距为$\frac{l}{2}$,现将单摆向左拉开一个小角度,然后无初速地释放,若小球碰撞时无能量损失,小球可视为质点,对于以后的运动,下列说法中正确的是( )| A. | 此组合摆周期为$\frac{{({\sqrt{2}+2})π}}{2}\sqrt{\frac{l}{g}}$,且每次碰撞一定发生在悬点正下方 | |
| B. | 摆球在平衡位置左右两侧走过的最大弧长相等 | |
| C. | 摆球在左侧上升的最大高度比右侧高 | |
| D. | 摆线在平衡位置右侧的最大摆角是左侧的二倍 |
 如图所示轻绳AD跨过固定在水平横梁BC右端的定滑轮挂住一个质量为M=10kg的物体,∠ACB=30°,g取10m/s2,求:
如图所示轻绳AD跨过固定在水平横梁BC右端的定滑轮挂住一个质量为M=10kg的物体,∠ACB=30°,g取10m/s2,求: 如图所示,物体A重40N,物体B重20N,A与B、B与地面间的动摩擦因数均为0.4,当用水平力向右匀速拉动物体A时,要求:
如图所示,物体A重40N,物体B重20N,A与B、B与地面间的动摩擦因数均为0.4,当用水平力向右匀速拉动物体A时,要求: