题目内容
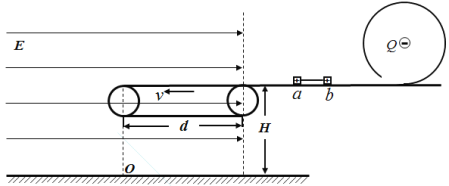
【题目】如图,高H=5m的光滑水平台左端有一逆时针转动的传送带(轮子大小可忽略不计),带的表面与平台等高,带长为d=1.25m,传送带左端正下方为O点。虚线左侧存在水平向右的匀强电场,大小为E=105N/C。平台右侧连接一光滑绝缘圆轨道,半径为R=1m,圆轨道中心固定一带负电的点电荷,电量为Q=104C。由于某种作用,使得电荷Q产生的电场只分布在圆轨道内部。可视为质点的绝缘带电滑块a、b用一轻质细绳连接,开始时整个装置处于静止状态。某时刻细线忽然断开,由于库仑斥力a、b反向运动,当滑块a进入传送带或者b进入圆轨道后即可忽略它们之间的斥力。已知滑块a、b的质量分别为m1=2 kg,m2=1kg,电量分别为q1=+6×105C和q2=+![]() ×105C,a进入传送带的速度为v1=4m/s,a与传送带之间的动摩擦因数μ=0.3, g=10 m/s2,静电力常量k=9×109N﹒m2/C2,空气阻力不计。求:
×105C,a进入传送带的速度为v1=4m/s,a与传送带之间的动摩擦因数μ=0.3, g=10 m/s2,静电力常量k=9×109N﹒m2/C2,空气阻力不计。求:
(1)滑块b进入圆轨道时的速度大小v2;
(2)滑块b到达圆轨道最高点时对轨道的压力;
(3)试分析传送带的速度v取不同值时,滑块a离开传送带后的落点与O点的位置关系。
【答案】(1)8m/s;(2)8N,方向竖直向上。(3)见解析所示
【解析】
(1)对ab,动量守恒,有
m1v1=m2v2
解得
v2=8m/s
(2)设b到最高点速度为v,受轨道压力为F,则有
![]()
从圆轨道最低点到最高点,有
![]()
解得
F=8N
由牛三,滑块对轨道的压力大小为F=F=8N,方向竖直向上。
(3)由题
q1E=μm1g=6N
离开传送带到落地的时间为
![]()
离开后水平方向的加速度为
![]() (向左)
(向左)
①若v>v1=4m/s,则滑块在带上匀速,以v1离开,离开后水平方向匀减速。
故水平位移为![]() 。故滑块落点位置为O点左侧2.5m处。
。故滑块落点位置为O点左侧2.5m处。
若v≤v1=4m/s,则滑块将减速,设全程减速到左端时速度为v1,则有
v1′2 v12=2a′d
其中
![]()
联立解得
v1′=1 m/s
②故当v< v1′=1 m/s时,物块全程减速,以v1′离开。
则水平位移为![]() 。故滑块落点位置为O点右侧0.5m处。
。故滑块落点位置为O点右侧0.5m处。
③当1m/s <v<4 m/s时,滑块与带共速离开。
则滑块落点与O点的距离为 ![]()
显然,当v=![]() m/s时,滑块落在O点;
m/s时,滑块落在O点;
当1m/s <v<![]() m/s时,滑块落在O点右侧。
m/s时,滑块落在O点右侧。
当![]() m/s <v< 4m/s时,滑块落在O点左侧。
m/s <v< 4m/s时,滑块落在O点左侧。

 阅读快车系列答案
阅读快车系列答案