题目内容
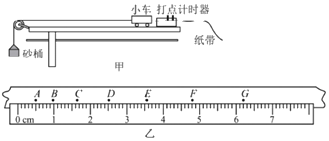
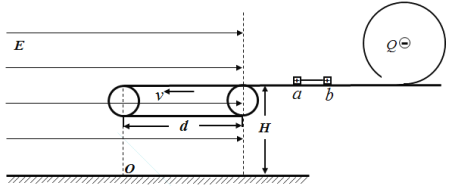
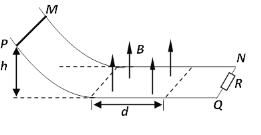
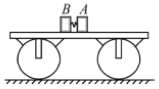
【题目】光滑水平面上有一质量m车=1.0kg的平板小车,车上静置A、B两物块。物块由轻质弹簧无栓接相连(物块可看作质点),质量分别为mA=1.0kg,mB=1.0kg。A距车右端x1(x1>1.5m),B距车左端x2=1.5m,两物块与小车上表面的动摩擦因数均为μ=0.1.车离地面的高度h=0.8m,如图所示。某时刻,将储有弹性势能Ep=4.0J的轻弹簧释放,使A、B瞬间分离,A、B两物块在平板车上水平运动。重力加速度g取10m/s2,求:
(1)弹簧释放瞬间后A、B速度的大小;
(2)B物块从弹簧释放后至落到地面上所需时间;
(3)若物块A最终并未落地,则平板车的长度至少多长?滑块在平板车上运动的整个过程中系统产生的热量多少?
【答案】(1)2m/s、2m/s;(2)1.4s;(3)3.25m ;3.25J。
【解析】
(1)释放弹簧过程A、B系统动量守恒、机械能守恒,
以向右为正方向,由动量守恒定律得:
mAvA﹣mBvB=0
由机械能守恒定律得:
![]()
代入数据解得:
vA=2m/s
vB=2m/s;
(2)由于A、B质量相等与桌面的动摩擦因数相等,在B在平板车上运动到左端过程小车所受合力为零,小车静止,B运动到小车左端过程,对B,由动能定理得:
![]()
由动量定理得:
﹣μmBgt1=mBvB﹣mBv2,
代入数据解得:
vB=1m/s
t1=1s,
B离开平板车后做平抛运动,竖直方向:
![]() ,
,
代入数据解得:
t2=0.4s,
运动时间:
t=t1+t2=1.4s;
(3)B离开小车时:vA=vB=1m/s,B离开平板车后,A与平板车组成的系统动量守恒,
以向右为正方向,由动量守恒定律得:
mAvA=(mA+m车)v
由能量守恒定律得:
![]()
代入数据解得:
L相对=0.25m;
A、B同时在小车上运动时小车不动,B滑出小车时,A在小车上滑行的距离与B在小车上滑行的距离相等为1.5m,小车的最小长度:
L=1.5+1.5+0.25=3.25m,
系统产生的热量:
E=μmAgx1+μmBgx2=3.25J;

 口算题天天练系列答案
口算题天天练系列答案