【题目】“难度系数”反映试题的难易程度，难度系数越大，题目得分率越高，难度也就越小．“难度系数”的计算公式为，其中，为难度系数，为样本平均失分，为试卷总分（一般为100分或150分）．某校高三年级的李老师命制了某专题共5套测试卷（每套总分150分），用于对该校高三年级480名学生进行每周测试．测试前根据自己对学生的了解，预估了每套试卷的难度系数，如下表所示：

测试后，随机抽取了50名学生的数据进行统计，结果如下：

（1）根据试卷2的难度系数估计这480名学生第2套试卷的平均分；

（2）从抽样的50名学生的5套试卷中随机抽取2套试卷，记这2套试卷中平均分超过96分的套数为，求的分布列和数学期望；

（3）试卷的预估难度系数和实测难度系数之间会有偏差．设为第套试卷的实测难度系数，并定义统计量，若，则认为本专题的5套试卷测试的难度系数预估合理，否则认为不合理．试检验本专题的5套试卷对难度系数的预估是否合理．

【题目】如图，在直角梯形中，，，平面平面，，，分别在线段和上，且，是等腰直角三角形．

（1）若，求证：平面．

（2），是否存在，使得与平面所成的角的正弦值为？若存在，求出的值；若不存在，请说明理由．

【题目】古希腊数学家阿波罗尼奥斯在他的著作《圆锥曲线论》中记载了用平面切制圆锥得到圆锥曲线的方法.如图，将两个完全相同的圆锥对顶放置（两圆锥的轴重合），已知两个圆锥的底面半径为1，母线长均为，记过圆锥轴的平面ABCD为平面（与两个圆锥面的交线为AC、BD），用平行于的平面截圆锥，该平面与两个圆锥侧面的截线即为双曲线E的一部分，且双曲线E的两条渐近线分别平行于AC、BD，则双曲线E的离心率为（ ）

A.B.C.D.2

(1)求m的值；

(2)若a，b均为正实数，且满足a＋b＝m，求a2＋b2的最小值．

（1）求在未来3天中，至少有1天下午4点前的销售量不少于450千克的概率．

（2）若该生鲜批发店以当天利润期望值为决策依据，当购进450千克比购进500千克的利润期望值大时，求x的取值范围．

【题目】如图，在直角梯形中，，，，，是的中点，是与的交点．将沿折起到的位置，如图．

（Ⅰ）证明：平面；

（Ⅱ）若平面平面，求平面与平面夹角的余弦值．

【题目】“柯西不等式”是由数学家柯西在研究数学分析中的“流数”问题时得到的，但从历史的角度讲，该不等式应当称为柯西﹣﹣布尼亚科夫斯基﹣﹣施瓦茨不等式，因为正是后两位数学家彼此独立地在积分学中推而广之，才将这一不等式推广到完善的地步，在高中数学选修教材4﹣5中给出了二维形式的柯西不等式：（a2+b2）（c2+d2）≥（ac+bd）2当且仅当ad＝bc（即）时等号成立．该不等式在数学中证明不等式和求函数最值等方面都有广泛的应用．根据柯西不等式可知函数的最大值及取得最大值时x的值分别为（　　）

A.B.C.D.

A. 1盏 B. 3盏 C. 5盏 D. 9盏

A. 各月的平均最低气温都在0℃以上

B. 七月的平均温差比一月的平均温差大

C. 三月和十一月的平均最高气温基本相同

D. 平均最高气温高于20℃的月份有5个

【题目】某城市208年抽样100户居民的月均用电量（单位：千瓦时），以，，，，，，分组，得到如下频率分布表：

（1）求表中的值，并估计2018年该市居民月均用电量的中位数；

（2）该城市最近十年的居民月均用电量逐年上升，以当年居民月均用电量的中位数（单位：千瓦时）作为统计数据，下图是部分数据的折线图．

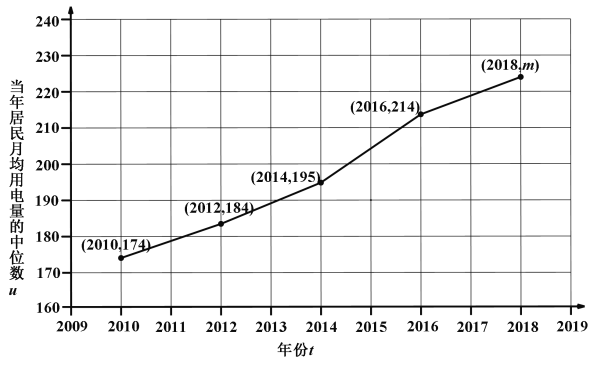
由折线图看出，可用线性回归模型拟合与年份的关系．

①为简化运算，对以上数据进行预处理，令，，请你在答题卡上完成数据预处理表；

②建立关于的线性回归方程，预测2020年该市居民月均用电量的中位数．

附：回归直线的斜率和截距的最小二乘估计公式分别为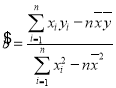：，．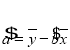