题目内容
【题目】如图,在直角梯形![]() 中,
中,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 分别在线段
分别在线段![]() 和
和![]() 上,且
上,且![]() ,
,![]() 是等腰直角三角形.
是等腰直角三角形.
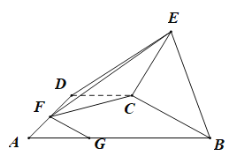
(1)若![]() ,求证:
,求证:![]() 平面
平面![]() .
.
(2)![]() ,是否存在
,是否存在![]() ,使得
,使得![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)证明见解析;(2)存在,![]()
【解析】
(1)根据题意分析可得![]() 是等腰三角形,可得
是等腰三角形,可得![]() ,进而可得
,进而可得![]() ,进而可得
,进而可得![]() ,即可得到结论;
,即可得到结论;
(2)根据题意,建立空间直角坐标系,得![]() ,
,![]() ,
,![]() ,进而可得平面
,进而可得平面![]() 的一个法向量,再利用
的一个法向量,再利用![]() ,得方程
,得方程![]() 解得即可得到结论.
解得即可得到结论.
(1)连接![]() ,
,![]() ,
,![]() .
.
又![]() 是等腰三角形,
是等腰三角形,![]() .
.
在直角梯形![]() 中,
中,![]() ,故
,故![]() 为直角三角形,
为直角三角形,
在![]() 中,
中,![]() ,
,
![]() ,
,![]() ,
,![]() 在
在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() ,故
,故![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
(2)如图,过![]() 作
作![]() 且
且![]() ,连接
,连接![]() 得四边形
得四边形![]() 为矩形.以
为矩形.以![]() 为原点,
为原点,![]() ,
,![]() 的方向为
的方向为![]() 轴,
轴,![]() 轴的正方向建立如图所示空间直角坐标系
轴的正方向建立如图所示空间直角坐标系![]() ,
,
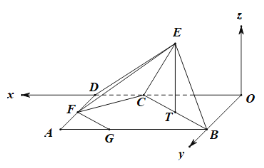
则![]() ,
,![]() ,
,![]() .
.
设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,
![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则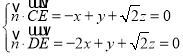
令![]() ,得
,得![]() .
.
设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则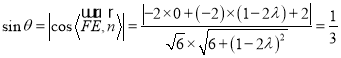 ,
,
化简得![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
![]() 存在实数
存在实数![]() ,使得
,使得![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,此时
,此时![]() .
.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
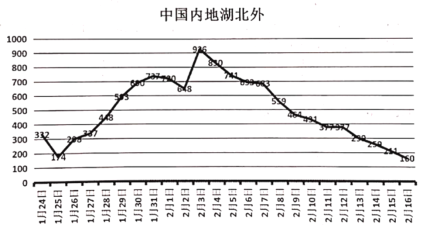
波波熊暑假作业江西人民出版社系列答案【题目】2019年春节前后,中国爆发新型冠状病毒(SARS-Cov-2)如图所示为1月24日至2月16日中国内地(除湖北以外的)感染新型冠状病毒新增人数的折线图,为了预测分析数据的变化规律,建立了![]() 与时间变量
与时间变量![]() 的不同时间段的两个线性回归模型.根据1月24日至2月3日的数据(时间变量
的不同时间段的两个线性回归模型.根据1月24日至2月3日的数据(时间变量![]() 的值依次为1,2,3,4,5,6,7,8,9,10,11)建立模型①:
的值依次为1,2,3,4,5,6,7,8,9,10,11)建立模型①:![]() ;根据2月4日至2月16日的数据(时间变量
;根据2月4日至2月16日的数据(时间变量![]() 的值依次为12,13,14,15,16,17,18,19,20,21,22,23,24)建立模型②:
的值依次为12,13,14,15,16,17,18,19,20,21,22,23,24)建立模型②:![]() .
.
1月 24日 | 1月 25日 | 1月 26日 | 1月 27日 | 1月 28日 | 1月 29日 | 1月 30日 | 1月 31日 | 2月 1日 | 2月 2日 | 2月 3日 |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
332 | 174 | 298 | 337 | 448 | 593 | 690 | 737 | 720 | 648 | 926 |
2月 4日 | 2月 5日 | 2月 6日 | 2月 7日 | 2月 8日 | 2月 9日 | 2月 10日 | 2月 11日 | 2月 12日 | 2月 13日 | 2月 14日 | 2月 15日 | 2月 16日 |
12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
830 | 741 | 693 | 683 | 559 | 464 | 431 | 377 | 377 | 299 | 259 | 211 | 160 |
(1)求出两个回归直线方程;(计算结果取整数)
(2)中国政府为了人民的生命安全,听取专家意见,了解了病毒信息,并迅速做出一系列的隔离防护措施,但新冠状病毒在世界范围内爆发时,某些欧美国家采取放任的态度,不治疗、不隔离、不检测,甚至不公布,请你用以上数据说明采取一系列措施的必要性,不采取措施的后果.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
参考公式: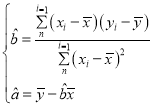 .
.
【题目】干支历法是上古文明的产物,又称节气历或中国阳历,是一部深奥的历法.它是用60组各不相同的天干地支标记年月日时的历法.具体的算法如下:先用年份的尾数查出天干,如2013年3为癸;再用2013年除以12余数为9,9为巳.那么2013年就是癸巳年了,
天干 | 甲 | 乙 | 丙 | 丁 | 戊 | 己 | 庚 | 辛 | 壬 | 癸 | ||
4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 | 2 | 3 | |||
地支 | 子 | 丑 | 寅 | 卯 | 辰 | 巳 | 午 | 未 | 申 | 酉 | 戌 | 亥 |
4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 1 | 2 | 3 |
2020年高三应届毕业生李东是壬午年出生,李东的父亲比他大25岁.问李东的父亲是哪一年出生( )
A.甲子B.乙丑C.丁巳D.丙卯