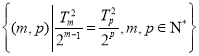��Ŀ����
����Ŀ��ij����208�����100��������¾��õ�������λ��ǧ��ʱ������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���飬�õ�����Ƶ�ʷֲ�����
���飬�õ�����Ƶ�ʷֲ�����
���� | Ƶ�� | Ƶ�� |
|
| 0.04 |
| 19 |
|
|
| 0.22 |
| 25 | 0.25 |
| 15 | 0.15 |
| 10 |
|
| 5 | 0.05 |
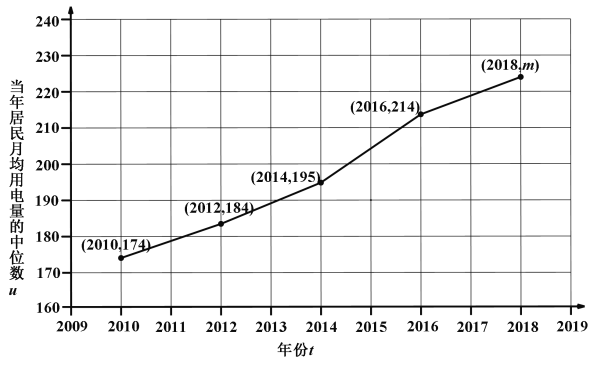
��1�������![]() ��ֵ��������2018����о����¾��õ�������λ��
��ֵ��������2018����о����¾��õ�������λ��![]() ��
��
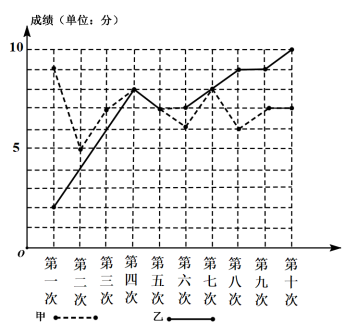
��2���ó������ʮ��ľ����¾��õ��������������Ե�������¾��õ�������λ��![]() ����λ��ǧ��ʱ����Ϊͳ�����ݣ���ͼ�Dz������ݵ�����ͼ��
����λ��ǧ��ʱ����Ϊͳ�����ݣ���ͼ�Dz������ݵ�����ͼ��
������ͼ�������������Իع�ģ�����![]() �����
�����![]() �Ĺ�ϵ��
�Ĺ�ϵ��
��Ϊ�����㣬���������ݽ���Ԥ��������![]() ��
��![]() �������ڴ�����������Ԥ��������
�������ڴ�����������Ԥ��������
�ڽ���![]() ����
����![]() �����Իع鷽�̣�Ԥ��2020����о����¾��õ�������λ����
�����Իع鷽�̣�Ԥ��2020����о����¾��õ�������λ����
�����ع�ֱ��![]() ��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��
��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��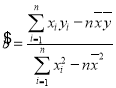 ��
��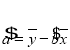 ��
��
���𰸡���1��![]() ��
��![]() ��
��![]() ��
��![]() �����
����λ��![]() ǧ��ʱ����2���ټ���������
ǧ��ʱ����2���ټ���������![]() ��237.2ǧ��ʱ.
��237.2ǧ��ʱ.
��������
��1������Ƶ�ʵ���Ƶ�������������ıȣ����![]() .������λ�����������Ƶ����ȣ������λ����
.������λ�����������Ƶ����ȣ������λ����
��2���ٸ�������ͼ�������Ԥ�������������ݲο���ʽ���![]() ����
����![]() �����Իع鷽�̣���
�����Իع鷽�̣���![]() ���ɵ�Ԥ��ֵ.
���ɵ�Ԥ��ֵ.
��1������֪��![]() ��ͬ��
��ͬ��![]() ��
��
![]() ��ͬ��
��ͬ��![]() ��
��
������Ƶ�ʷֲ�������λ��Ϊ![]() ����
����
![]() �����
�����![]() ��
��
�������������壬�ɹ���2018����о����¾��õ�������λ��![]() ǧ��ʱ��
ǧ��ʱ��
��2��������Ԥ���������£�
|
|
| 0 | 2 | 4 |
|
|
| 0 | 19 | 29 |
���ɢٿ�֪��![]() ��
��![]() ��
��
��![]() ����
����![]() �����Իع鷽��Ϊ
�����Իع鷽��Ϊ![]() ����
����
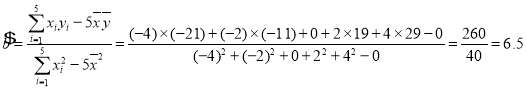 ��
��
��![]() ��
��
��![]() ��
��
����![]() ��
��![]() ����
����![]() ��
��
������![]() ����
����![]() �����Իع鷽��Ϊ��
�����Իع鷽��Ϊ��![]() ��
��
��![]() ��
��
��Ԥ�����2020������¾��õ�������λ��Ϊ
![]() ��ǧ��ʱ����
��ǧ��ʱ����

����Ŀ��2020��������ʼ������״�����������ڣ�����ʹ�ø���ѧ���ں��ٽ���֮������У���������ʹ���������Ͻ�ѧ��Զ�̽�ѧ��ͣ�β�ͣѧ��Ҫ��Ҳ�õ��˼ҳ��ǵ���ͬ������ѧУ��չ��ʽ���������Ͻ�ѧ��ij��ѧУΪ�˼�ǿѧ����������������ѧ�Σ�Ϊ���˽�ѧ��ϲ����ѧ�Ƿ����Ա��йأ���ѧУ��100��ѧ���������ʾ����飬�õ�������������
ϲ����ѧ | ��ϲ����ѧ | �ϼ� | |
���� | 20 | 50 | |
�� | 10 | ||
�ϼ� | 100 |
��1���뽫�����������������������ж��ܷ��ڷ�����ĸ��ʲ�����0.001��ǰ������Ϊϲ����ѧ���Ա��й�ϵ��
��2������ʾ������100��ѧ����ѧУ������ϲ����ѧ�����а��ֲ�����ķ��������ȡ6�˳�����ѧ�����飬������6������ѡ2����Ϊ��������鳤������������Ů������Ϊ![]() ����
����![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
�ο����ݣ�
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
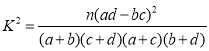 ��
��![]() ��
��
����Ŀ��ij����������ÿ����߲�����������5Ԫ/ǧ�˹���ij����ɫ�߲ˣ��ۼ�8Ԫ/ǧ�ˣ���ÿ������4����ǰ����������ɫ�߲�û�����꣬���δ�۳�����ɫ�߲˽��۴�������3Ԫ/ǧ�˳��ۣ����ݾ��飬���ۺ��ܹ���ʣ���߲�ȫ��������ϣ��ҵ��첻�ٽ����������������������˹���30�죨ÿ������4����ǰ��������ɫ�߲˵�������������λ��ǧ�ˣ��õ�����ͳ�����ݣ���Ƶ��Ϊ���ʣ���ע��x��y��N*��
ÿ������4��ǰ������ | 350 | 400 | 450 | 500 | 550 |
���� | 3 | 9 | x | y | 2 |
��1������δ��3���У�������1������4��ǰ��������������450ǧ�˵ĸ��ʣ�
��2�����������������Ե�����������ֵΪ�������ݣ�������450ǧ�˱ȹ���500ǧ�˵���������ֵ��ʱ����x��ȡֵ��Χ��