【题目】为了解某地网民浏览购物网站的情况,从该地随机抽取100名网民进行调查,其中男性、女性人数分别为60和40.下面是根据调查结果统计的数据,将日均浏览购物网站时间不低于40分钟的网民称为“网购达人”,已知“网购达人”中女性人数为15人.
日均浏览购物网站时间(分钟) |
|
|
|
|
|
|
人数 | 2 | 14 | 24 | 35 | 20 | 5 |
(1)根据已知条件完成下面的![]() 列联表,并判断是否有99%的把握认为是否为“网购达人”与性别有关;
列联表,并判断是否有99%的把握认为是否为“网购达人”与性别有关;
非网购达人 | 网购达人 | 总计 | |
男 | |||
女 | 15 | ||
总计 |
(2)从上述调查中的“网购达人”中按性别分层抽样,抽取5人发放礼品,再从这5人中随机选出2人作为“最美网购达人”,求这两个“最美网购达人”中恰好为1男1女的概率.
参考公式: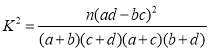 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】为了解某地网民浏览购物网站的情况,从该地随机抽取100名网民进行调查,其中男性、女性人数分别为45和55.下面是根据调查结果绘制的网民日均浏览购物网站时间的频率分布直方图,将日均浏览购物网站时间不低于40分钟的网民称为“网购达人”,已知“网购达人”中女性有10人.

(1)根据已知条件完成下面的![]() 列联表,并判断是否有90%的把握认为是否为“网购达人”与性别有关;
列联表,并判断是否有90%的把握认为是否为“网购达人”与性别有关;
非网购达人 | 网购达人 | 总计 | |
男 | |||
女 | 10 | ||
总计 |
(2)将上述调査所得到的频率视为概率,现在从该地的网民中随机抽取3名,记被抽取的3名网民中的“网购达人”的人数为X,求X的分布列、数学期望![]() 和方差
和方差![]() .
.
参考公式: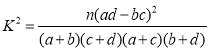 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某公司培训员工某项技能,培训有如下两种方式:
方式一:周一到周五每天培训1小时,周日测试
方式二:周六一天培训4小时,周日测试
公司有多个班组,每个班组60人,现任选两组![]() 记为甲组、乙组
记为甲组、乙组![]() 先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
第一周 | 第二周 | 第三周 | 第四周 | |
甲组 | 20 | 25 | 10 | 5 |
乙组 | 8 | 16 | 20 | 16 |
![]() 用方式一与方式二进行培训,分别估计员工受训的平均时间
用方式一与方式二进行培训,分别估计员工受训的平均时间![]() 精确到
精确到![]() ,并据此判断哪种培训方式效率更高?
,并据此判断哪种培训方式效率更高?
![]() 在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.