题目内容
【题目】某连锁超市旗舰店在元旦当天推出一个购物满百元抽奖活动，凡是一次性购物满百元者可以从抽奖箱中一次性任意摸出2个小球（抽奖箱内共有5个小球，每个小球大小形状完全相同，这5个小球上分别标有1，2，3，4，5 这5个数字）.
（1）列出摸出的2个小球的所有可能的结果.
（2）已知该超市活动规定：摸出的2个小球都是偶数为一等奖；摸出的2个小球都是奇数为二等奖.请分别求获得一等奖的概率与获得二等奖的概率.
【答案】（1）所有可能的结果为
，
，
，
，
，
，
，
，
，
.（2）获得一等奖的概率为
.获得二等奖的概率为
.
【解析】
（1）根据题意，从
个球中任取
个，简单列举即可；
（2）根据（1）中所求，找出满足题意的可能性个数，即可由古典概型的概率计算公式求得结果.
（1）摸出的2个小球的所有可能的结果为，，，，，，，，，.
（2）由（1）知，摸出的2个小球的所有可能的结果共有10个，
摸出的2个小球都是偶数的所有可能的结果为，
所以获得一等奖的概率为.
摸出的2个小球都是奇数的所有可能的结果为，，，
所以获得二等奖的概率为.
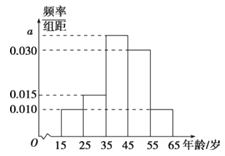
【题目】为了解某地网民浏览购物网站的情况，从该地随机抽取100名网民进行调查，其中男性、女性人数分别为45和55.下面是根据调查结果绘制的网民日均浏览购物网站时间的频率分布直方图，将日均浏览购物网站时间不低于40分钟的网民称为“网购达人”，已知“网购达人”中女性有10人.
（1）根据已知条件完成下面的
列联表，并判断是否有90%的把握认为是否为“网购达人”与性别有关；
非网购达人 | 网购达人 | 总计 | |
男 | |||
女 | 10 | ||
总计 |
（2）将上述调査所得到的频率视为概率，现在从该地的网民中随机抽取3名，记被抽取的3名网民中的“网购达人”的人数为X，求X的分布列、数学期望
和方差
.
参考公式：
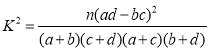，其中
.
参考数据：
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
