【题目】某校为了了解学生对消防知识的了解情况,从高一年级和高二年级各选取100名同学进行消防知识竞赛.下图(1)和图(2)分别是对高一年级和高二年级参加竞赛的学生成绩按![]() 分组,得到的频率分布直方图.
分组,得到的频率分布直方图.
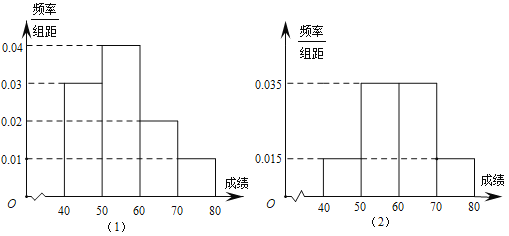
(1)请计算高一年级和高二年级成绩小于60分的人数;
(2)完成下面![]() 列联表,并回答:有多大的把握可以认为“学生所在的年级与消防常识的了解存在相关性”?
列联表,并回答:有多大的把握可以认为“学生所在的年级与消防常识的了解存在相关性”?
成绩小于60分人数 | 成绩不小于60分人数 | 合计 | |
高一 | |||
高二 | |||
合计 |
附:临界值表及参考公式:![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】据气象局统计,某市2019年从1月1日至1月30日这30天里有26天出现雾霾天气.国际上通常用环境空气质量指数(AQI)来描述污染状况,下表是某气象观测点记录的连续4天里,该市AQI指数![]() 与当天的空气水平可见度
与当天的空气水平可见度![]() 的情况.
的情况.
AQI指数 | 900 | 700 | 300 | 100 |
空气水平可见度 | 0.5 | 3.5 | 6.5 | 9.5 |
(1)设![]() ,根据表中的数据,求出
,根据表中的数据,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)若某天该市AQT指数![]() ,那么当天空气水平可见度大约为多少?
,那么当天空气水平可见度大约为多少?
附:参考数据:![]() ,
,![]() .
.
参考公式:线性回归力程![]() 中,
中,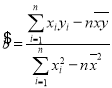 ,
,![]() ,其中
,其中![]() 为样本平均数.
为样本平均数.
【题目】甲、乙两家物流公司都需要进行货物中转,由于业务量扩大,现向社会招聘货车司机,其日工资方案如下:甲公司,底薪80元,司机毎中转一车货物另计4元:乙公司无底薪,中转40车货物以内(含40车)的部分司机每车计6元,超出40车的部分司机每车计7元.假设同一物流公司的司机一填中转车数相同,现从这两家公司各随机选取一名货车司机,并分别记录其50天的中转车数,得到如下频数表:
甲公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 10 | 15 | 10 | 10 | 5 |
乙公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 5 | 10 | 10 | 20 | 5 |
(1)现从记录甲公司的50天货物中转车数中随机抽取3天的中转车数,求这3天中转车数都不小于40的概率;
(2)若将频率视为概率,回答下列两个问题:
①记乙公司货车司机日工资为X(单位:元),求X的分布列和数学期望E(X);
②小王打算到甲、乙两家物流公司中的一家应聘,如果仅从日工资的角度考虑,请利用所学的统计学知识为小王作出选择,并说明理由.