题目内容
【题目】已知函数![]() 有两个不同的极值点x1,x2,且x1<x2.
有两个不同的极值点x1,x2,且x1<x2.
(1)求实数a的取值范围;
(2)求证:x1x2<a2.
【答案】(1)(e,+∞);(2)见解析
【解析】
(1)先求导数,再根据导函数有两个不同的零点,确定实数a所需满足的条件,解得结果,(2)先根据极值点解得a,再代入化简不等式x1x2<a2,设![]() ,构造一元函数,利用导数研究函数单调性,最后构造单调性证明不等式.
,构造一元函数,利用导数研究函数单调性,最后构造单调性证明不等式.
(1)∵函数![]() ,∴x>0,f′(x)=x-alnx,
,∴x>0,f′(x)=x-alnx,
∵函数![]() 有两个不同的极值点x1,x2,且x1<x2.
有两个不同的极值点x1,x2,且x1<x2.
∴f′(x)=x-alnx=0有两个不等根,
令g(x)=x-alnx,则![]() =
=![]() ,(x>0),
,(x>0),
①当a≤0时,得g′(x)>0,则g(x)在(0,+∞)上单调递增,
∴g(x)在(0,+∞)上不可能有两个零点.
②当a>0时,由g′(x)>0,解得x>a,由g′(x)<0,解得0<x<a,
则g(x)在(0,a)上单调递减,在(a,+∞)上单调递增,
要使函数g(x)有两个零点,则g(a)=a-alna<0,
解得a>e,∴实数a的取值范围是(e,+∞).
(2)由x1,x2是g(x)=x-alnx=0的两个根,
则 ,两式相减,得a(lnx2-lnx1)=x2-x1),
,两式相减,得a(lnx2-lnx1)=x2-x1),
即a=![]() ,即证x1x2<
,即证x1x2<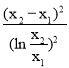 ,
,
即证![]() =
=![]() ,
,
由x1<x2,得![]() =t>1,只需证ln2t-t-
=t>1,只需证ln2t-t-![]() ,
,
设g(t)=ln2t-t-![]() ,则g′(t)=
,则g′(t)=![]() =
=![]() ,
,
令h(t)=2lnt-t+![]() ,∴h′(t)=
,∴h′(t)=![]() =-(
=-(![]() )2<0,
)2<0,
∴h(t)在(1,+∞)上单调递减,∴h(t)<h(1)=0,
∴g′(t)<0,即g(t)在(1,+∞)上是减函数,∴g(t)<g(1)=0,
即ln2t<t-2+![]() 在(1,+∞)上恒成立,∴x1x2<a2.
在(1,+∞)上恒成立,∴x1x2<a2.

 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案【题目】据气象局统计,某市2019年从1月1日至1月30日这30天里有26天出现雾霾天气.国际上通常用环境空气质量指数(AQI)来描述污染状况,下表是某气象观测点记录的连续4天里,该市AQI指数![]() 与当天的空气水平可见度
与当天的空气水平可见度![]() 的情况.
的情况.
AQI指数 | 900 | 700 | 300 | 100 |
空气水平可见度 | 0.5 | 3.5 | 6.5 | 9.5 |
(1)设![]() ,根据表中的数据,求出
,根据表中的数据,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)若某天该市AQT指数![]() ,那么当天空气水平可见度大约为多少?
,那么当天空气水平可见度大约为多少?
附:参考数据:![]() ,
,![]() .
.
参考公式:线性回归力程![]() 中,
中,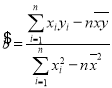 ,
,![]() ,其中
,其中![]() 为样本平均数.
为样本平均数.
【题目】某超市计划按月订购一种酸奶,每天进货量相同,已知每售出一箱酸奶的利润为50元,当天未售出的酸奶降价处理,以每箱亏损10元的价格全部处理完.若供不应求,可从其它商店调拨,每销售1箱可获利30元.假设该超市每天的进货量为14箱,超市的日利润为![]() 元.为确定以后的订购计划,统计了最近50天销售该酸奶的市场日需求量,其频率分布表如图所示.
元.为确定以后的订购计划,统计了最近50天销售该酸奶的市场日需求量,其频率分布表如图所示.
序号 | 分组 | 频数(天) | 频率 |
1 |
|
| 0.16 |
2 |
| 12 |
|
3 |
|
| 0.3 |
4 |
|
|
|
5 |
| 5 | 0.1 |
合计 | 50 | 1 | |
(1)求![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)求![]() 关于日需求量
关于日需求量![]() 的函数表达式;
的函数表达式;
(3)以50天记录的酸奶需求量的频率作为酸奶需求量发生的概率,估计日利润在区间![]() 内的概率.
内的概率.
