题目内容
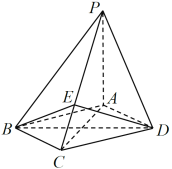
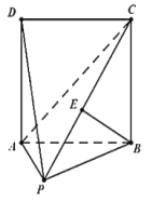
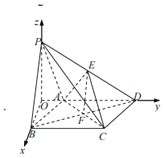
【题目】如图,在四棱锥P-ABCD中,底而ABCD是菱形,且PA=AD=2,∠PAD=∠BAD=120°,E,F分别为PD,BD的中点,且![]() .
.
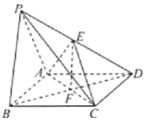
(1)求证:平面PAD⊥平面ABCD;
(2)求锐二面角E-AC-D的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)先过P作PO⊥AD,再通过平几知识计算得PO⊥BO,利用线面垂直判定定理得PO⊥平面ABCD,再根据面面垂直判定定理得结果,(2)先根据条件建立空间直角坐标系,设立各点坐标,列方程组解得平面ACE的一个法向量,根据向量数量积得向量夹角,最后根据二面角与向量夹角关系得结果.
(1)过P作PO⊥AD,垂足为O,连结AO,BO,
由∠PAD=120°,得∠PAO=60°,
∴在Rt△PAO中,PO=PAsin∠PAO=2sin60°=2×![]() =
=![]() ,
,
∵∠BAO=120°,∴∠BAO=60°,AO=AO,∴△PAO≌△BAO,∴BO=PO=![]() ,
,
∵E,F分别是PA,BD的中点,EF=![]() ,∴EF是△PBD的中位线,
,∴EF是△PBD的中位线,
∴PB=2EF=2×![]() =
=![]() ,
,
∴PB2=PO2+BO2,∴PO⊥BO,∵AD∩BO=O,∴PO⊥平面ABCD,
又PO平面PAD,∴平面PAD⊥平面ABCD.
(2)以O为原点,OB为x轴,OD为y轴,OP为z轴,建立空间直角坐标系,
A(0,1,0),P(0,0,![]() ),B(
),B(![]() ,0,0),D(0,3,0),
,0,0),D(0,3,0),
∴E(0,![]() ),F(
),F(![]() ,
,![]() ),
),![]() =(0,
=(0,![]() ),
),![]() =(
=(![]() ,
,![]() ,0),
,0),
易得平面ABCD的一个法向量![]() =
=
设平面ACE的法向量![]() =(x,y,z),则
=(x,y,z),则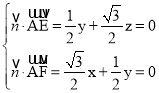 ,
,
取x=1,得![]() =(1,-
=(1,-![]() ,1),
,1),
设锐二面角的平面角的大小为θ,则cosθ=|cos<![]() >|=
>|=![]() =
=![]() ,
,
∴锐二面角E-AC-D的余弦值为![]() .
.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目