3.设数列{an}的前n项和为Sn.且a1+2a23a3+…+nan=(n-1)Sn+2n(n∈N*).
(1)求a1,a2的值;
(2)求证:数列{Sn+2}是等比数列;
(3)求数列{an}的通项公式.
(1)求a1,a2的值;
(2)求证:数列{Sn+2}是等比数列;
(3)求数列{an}的通项公式.
2.函数f(x)=ax2-x是R上的减函数,则( )
| A. | a=0 | B. | a<1 | C. | a<0 | D. | a≤1 |
18.函数y=$\sqrt{-sinx}$+$\sqrt{tanx}$的定义域是( )
0 251751 251759 251765 251769 251775 251777 251781 251787 251789 251795 251801 251805 251807 251811 251817 251819 251825 251829 251831 251835 251837 251841 251843 251845 251846 251847 251849 251850 251851 251853 251855 251859 251861 251865 251867 251871 251877 251879 251885 251889 251891 251895 251901 251907 251909 251915 251919 251921 251927 251931 251937 251945 266669
| A. | 2kπ+π≤x≤2kπ+$\frac{3π}{2}$,k∈Z | B. | 2kπ+π<x<2kπ+$\frac{3π}{2}$,k∈Z | ||
| C. | 2kπ+π≤x<2kπ+$\frac{3π}{2}$,k∈Z | D. | 2kπ+π<x<2kπ+$\frac{3π}{2}$或x=kπ,k∈Z |
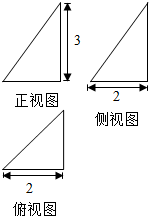 一个几何体的三视图是三个直角三角形,尺寸如图所示,求表面积.
一个几何体的三视图是三个直角三角形,尺寸如图所示,求表面积.