16.设定义在R上的函数f(x)=$\left\{\begin{array}{l}{2(x=0)}\\{lo{g}_{3}|x|(x≠0)}\end{array}\right.$,若关于x的方程f2(x)+bf(x)+c=0恰有3个不同的实数解,则bc=( )
| A. | -9 | B. | 9 | C. | -16 | D. | 16 |
15.奇函数f(x)(x∈R)满足f(-4)=f(1)=0,且在区间(0,2]与[2,+∞)上分别是增函数和减函数,则满足x3•f(x)>0的x的取值范围是( )
| A. | (-4,-1)∪(1,4) | B. | (-∞,4)∪(-1,0) | C. | (-∞,-4)∪(4,+∞) | D. | (-∞,-4)∪(-1,0)∪(1,4) |
14.若函数f(x)同时满足:①对于定义域上的任意x,恒有f(x)+f(-x)=0;②对于定义域上的任意x1,x2,当x1≠x2时,恒有(x1-x2)[f(x1)-f(x2)]<0,则称函数f(x)为“优美函数”,则下列函数中是“优美函数”的是( )
| A. | f(x)=ex+e-x | B. | f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$ | ||
| C. | f(x)=lg($\sqrt{{x}^{2}+1}-x$) | D. | f(x)=$\left\{\begin{array}{l}{{x}^{2},}&{x≥0}\\{-{x}^{2},}&{x<0}\end{array}\right.$ |
13.已知1<x<10,令a=lgx,b=log2(lgx),c=2lgx,则a,b,c的大小关系是( )
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | b<c<a |
12.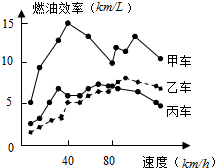 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三两汽车在不同速度下的燃油效率情况.某城市机动车最高限速80千米/小时,相同条件下,用甲、乙、丙三两汽车在该市行驶,最省油是( )
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三两汽车在不同速度下的燃油效率情况.某城市机动车最高限速80千米/小时,相同条件下,用甲、乙、丙三两汽车在该市行驶,最省油是( )
 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三两汽车在不同速度下的燃油效率情况.某城市机动车最高限速80千米/小时,相同条件下,用甲、乙、丙三两汽车在该市行驶,最省油是( )
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三两汽车在不同速度下的燃油效率情况.某城市机动车最高限速80千米/小时,相同条件下,用甲、乙、丙三两汽车在该市行驶,最省油是( )| A. | 甲车 | B. | 乙车 | C. | 丙车 | D. | 无法确定 |
11.若0<a<1,-1<b<0,则函数y=ax+b的图象必不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.已知f(x)=$\left\{\begin{array}{l}{x-4}&{(x≥6)}\\{f(x+3)}&{(x<6)}\end{array}\right.$,则f(1)为( )
| A. | 3 | B. | B、4 | C. | C5 | D. | 6 |
9.若函数f(x)是定义在R上的偶函数,在(-∞,0]上是减函数,且f(2)=0,则使得(x-2)f(x)<0的x的取值范围是( )
| A. | (-∞,-2) | B. | (2,+∞) | C. | (-∞,-2)∪(2,+∞) | D. | (-2,2) |
8.已知A=(a-1,a+2),B={x|x2-9x+18≤0},则能使B?A成立的实数a的取值范围是( )
0 251523 251531 251537 251541 251547 251549 251553 251559 251561 251567 251573 251577 251579 251583 251589 251591 251597 251601 251603 251607 251609 251613 251615 251617 251618 251619 251621 251622 251623 251625 251627 251631 251633 251637 251639 251643 251649 251651 251657 251661 251663 251667 251673 251679 251681 251687 251691 251693 251699 251703 251709 251717 266669
| A. | {a|a=4} | B. | {a|3≤a≤4} | C. | {a|3<a<4} | D. | Φ |