题目内容
9.若函数f(x)是定义在R上的偶函数,在(-∞,0]上是减函数,且f(2)=0,则使得(x-2)f(x)<0的x的取值范围是( )| A. | (-∞,-2) | B. | (2,+∞) | C. | (-∞,-2)∪(2,+∞) | D. | (-2,2) |
分析 根据f(x)的奇偶性及在(-∞,0]上的单调性可判断f(x)在(0,+∞)上的单调性,再由f(x)图象上的特殊点可作出f(x)在R上的草图,根据图象可解得不等式.
解答  解:∵f(x)是定义在R上的偶函数,在(-∞,0]上是减函数,
解:∵f(x)是定义在R上的偶函数,在(-∞,0]上是减函数,
∴f(x)在(0,+∞)上为增函数,
∵f(2)=0,∴f(-2)=f(2)=0,作出函数f(x)在R上的草图,如图所示:
由图象知,(x-2)f(x)<0?$\left\{\begin{array}{l}{x-2>0}\\{f(x)<0}\end{array}\right.$或$\left\{\begin{array}{l}{x-2<0}\\{f(x)>0}\end{array}\right.$?x<-2,
∴使得(x-2)f(x)<0的x的取值范围为(-∞,-2),
故选:A.
点评 本题考查函数的奇偶性、单调性及其应用,考查抽象不等式的求解,考查数形结合思想,考查学生综合运用知识解决问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.若函数f(x)同时满足:①对于定义域上的任意x,恒有f(x)+f(-x)=0;②对于定义域上的任意x1,x2,当x1≠x2时,恒有(x1-x2)[f(x1)-f(x2)]<0,则称函数f(x)为“优美函数”,则下列函数中是“优美函数”的是( )
| A. | f(x)=ex+e-x | B. | f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$ | ||
| C. | f(x)=lg($\sqrt{{x}^{2}+1}-x$) | D. | f(x)=$\left\{\begin{array}{l}{{x}^{2},}&{x≥0}\\{-{x}^{2},}&{x<0}\end{array}\right.$ |
18.已知集合M={x|0≤x≤2},N={x|x-2=0},则下列说法正确的是( )
| A. | N∈M | B. | N⊆M | C. | M⊆N | D. | M∈N |
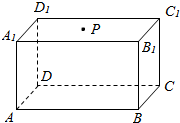 如图,P为长方体ABCD-A1B1C1D1的上底面A1B1C1D1内的一点,过直线BC与点P的平面记为α,若α∩平面A1B1C1D1=l
如图,P为长方体ABCD-A1B1C1D1的上底面A1B1C1D1内的一点,过直线BC与点P的平面记为α,若α∩平面A1B1C1D1=l