13.设0<θ<π,若cosθ+isinθ=$\frac{1+\sqrt{3}i}{-2i}$(i为虚数单位),则θ的值为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{π}{6}$ |
8.若x∈R,且满足$\frac{x}{4}+\frac{1}{x}$=sinθ,则θ的值等于( )
| A. | kπ+$\frac{π}{2}$(k∈Z) | B. | kπ(k∈Z) | C. | 2kπ+$\frac{π}{2}$(k∈Z) | D. | $\frac{1}{2}kπ$(k∈Z) |
7. 如图所示的算法流程图中,若f(x)=lnx,g(x)=log2x,则h(4)的值等于( )
如图所示的算法流程图中,若f(x)=lnx,g(x)=log2x,则h(4)的值等于( )
 如图所示的算法流程图中,若f(x)=lnx,g(x)=log2x,则h(4)的值等于( )
如图所示的算法流程图中,若f(x)=lnx,g(x)=log2x,则h(4)的值等于( )| A. | 1 | B. | -1 | C. | 2 | D. | ln4 |
6.已知f(x)是定义在R上的偶函数,且以2为周期,则“f(x)在[0,1]上递增”是“f(x)在[1,2]上递减”的( )
| A. | 既不充分也不必要条件 | B. | 充要条件 | ||
| C. | 必要而不充分条件 | D. | 充分而不必要条件 |
5.已知复数z=x+2i(x∈R,i为虚数单位),z2=-3+4i,则x=( )
| A. | ±1 | B. | -1 | C. | 0 | D. | 1 |
4.已知M(a,5-a,2a-1),N(1,a+2,2-a)两点,当|MN|取得最小值时,a的值是( )
0 250235 250243 250249 250253 250259 250261 250265 250271 250273 250279 250285 250289 250291 250295 250301 250303 250309 250313 250315 250319 250321 250325 250327 250329 250330 250331 250333 250334 250335 250337 250339 250343 250345 250349 250351 250355 250361 250363 250369 250373 250375 250379 250385 250391 250393 250399 250403 250405 250411 250415 250421 250429 266669
| A. | 19 | B. | $\frac{19}{14}$ | C. | -$\frac{8}{7}$ | D. | $\frac{8}{7}$ |
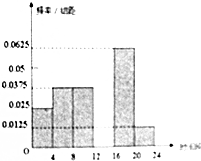 上饶市政府为缓解城市交通压力,计划对金龙岗路等交通要道由双向通行改为单项通行,为调查金龙岗路的通行能力,交警部门将某一天24小时分为六个时段,分别是[0,4)…[20,24)(小时),并记录每一时段通行此路的机动车的辆数,共计为600辆,绘制如下部分频率分布直方图,观察图形的信息,回答下列问题:
上饶市政府为缓解城市交通压力,计划对金龙岗路等交通要道由双向通行改为单项通行,为调查金龙岗路的通行能力,交警部门将某一天24小时分为六个时段,分别是[0,4)…[20,24)(小时),并记录每一时段通行此路的机动车的辆数,共计为600辆,绘制如下部分频率分布直方图,观察图形的信息,回答下列问题:
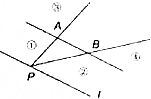 如图,点P是直线l上一点,l∥直线AB,如果存在实数x,y,使得$\overrightarrow{PC}=x\overrightarrow{PA}+y\overrightarrow{PB}$,且x+y=2,x>2,则点C所在的区域是图中标示的区域( )
如图,点P是直线l上一点,l∥直线AB,如果存在实数x,y,使得$\overrightarrow{PC}=x\overrightarrow{PA}+y\overrightarrow{PB}$,且x+y=2,x>2,则点C所在的区域是图中标示的区域( )