题目内容
8.若x∈R,且满足$\frac{x}{4}+\frac{1}{x}$=sinθ,则θ的值等于( )| A. | kπ+$\frac{π}{2}$(k∈Z) | B. | kπ(k∈Z) | C. | 2kπ+$\frac{π}{2}$(k∈Z) | D. | $\frac{1}{2}kπ$(k∈Z) |
分析 由基本不等式可得式子的取值范围,结合三角函数的值域可得sinθ=±1,可得θ取值.
解答 解:当x>0时,$\frac{x}{4}+\frac{1}{x}$≥2$\sqrt{\frac{x}{4}•\frac{1}{x}}$=1,
当且仅当$\frac{x}{4}$=$\frac{1}{x}$即x=2时取等号,
又sinθ∈[-1,1],∴sinθ=1;
同理当x<0时,可得sinθ=-1;
∴θ=kπ+$\frac{π}{2}$,k∈Z,
故选:A.
点评 本题考查基本不等式求最值,涉及三角函数的知识,属基础题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
16.半径为1的球内最大圆柱的体积为( )
| A. | $\frac{2\sqrt{6}}{9}$π | B. | $\frac{\sqrt{3}}{4}$π | C. | $\frac{2\sqrt{3}}{3}$π | D. | $\frac{4\sqrt{3}}{9}$π |
13.设0<θ<π,若cosθ+isinθ=$\frac{1+\sqrt{3}i}{-2i}$(i为虚数单位),则θ的值为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{π}{6}$ |
 已知正方体ABCD-A1B1C1D1.
已知正方体ABCD-A1B1C1D1. 如图所示,已知平面α∥平面β,AB与CD是两条异面直线且AB?α,CD?β,如果E、F、G分别是AC、CB、BD的中点.求证:平面EFG∥α∥β.
如图所示,已知平面α∥平面β,AB与CD是两条异面直线且AB?α,CD?β,如果E、F、G分别是AC、CB、BD的中点.求证:平面EFG∥α∥β.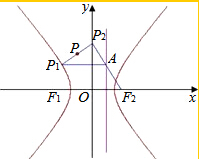 已知点P1(x0,y0)为双曲线$\frac{{x}^{2}}{8{b}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(b为正常数)上任一点,F2为双曲线的右焦点,过P作直线x=$\frac{8b}{3}$的垂线,垂足为A,连接F2A并延长交y轴于P2.
已知点P1(x0,y0)为双曲线$\frac{{x}^{2}}{8{b}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(b为正常数)上任一点,F2为双曲线的右焦点,过P作直线x=$\frac{8b}{3}$的垂线,垂足为A,连接F2A并延长交y轴于P2.