题目内容
9．
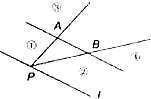如图，点P是直线l上一点，l∥直线AB，如果存在实数x，y，使得$\overrightarrow{PC}=x\overrightarrow{PA}+y\overrightarrow{PB}$，且x+y=2，x＞2，则点C所在的区域是图中标示的区域（ ）| A． | ① | B． | ② | C． | ③ | D． | ④ |
分析 根据条件容易判断出x＞0，y＜0，从而根据向量数乘的几何意义及向量加法的平行四边形法则即可找出点C所在区域是图中哪一区域．
解答 解：x+y=2，x＞2；
∴y＜0，x＞0；
∴根据向量加法的平行四边形法则知点C所在的区域是图中③标示的区域．
故选：C．
点评 考查向量数乘的几何意义，以及向量加法的平行四边形法则．
练习册系列答案
相关题目
20．设△ABC的内角A，B，C所对的边长分别为a，b，c，且atanB=$\frac{20}{3}$，bsinA=4，则a等于（ ）
| A． | 3 | B． | $\frac{8}{3}$ | C． | 4 | D． | 5 |
17．
如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（ ）
如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（ ）| A． | 2$\sqrt{5}$ | B． | 2$\sqrt{6}$ | C． | 4$\sqrt{2}$ | D． | 4$\sqrt{3}$ |
4．已知M（a，5-a，2a-1），N（1，a+2，2-a）两点，当|MN|取得最小值时，a的值是（ ）
| A． | 19 | B． | $\frac{19}{14}$ | C． | -$\frac{8}{7}$ | D． | $\frac{8}{7}$ |
14．若|$\overrightarrow{e}$|=1，且$\overrightarrow{a}⊥\overrightarrow{e}$，|$\overrightarrow{a}$|=2，则|4$\overrightarrow{a}-\overrightarrow{e}$|=（ ）
| A． | $\sqrt{37}$ | B． | $\sqrt{65}$ | C． | 8 | D． | $\sqrt{13}$ |