题目内容
10.已知某三棱锥的三视图如图所示,这这个三棱锥的体积是$\frac{64}{3}$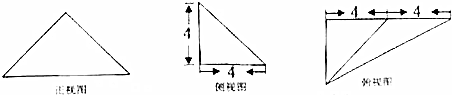
分析 根据几何体的三视图,得出该几何体是底面为直角三角形,高为4的三棱锥,再根据图中数据求出它的体积.
解答  解:根据几何体的三视图,得;
解:根据几何体的三视图,得;
该几何体是底面直角三角形,高为4的三棱锥,如图所示;
所以该三棱锥的体积为
V=$\frac{1}{3}$×$\frac{1}{2}$×8×4×4=$\frac{64}{3}$.
故答案为:$\frac{64}{3}$.
点评 本题考查了利用空间几何体三视图求体积的应用问题,是基础题目.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
1.已知非零向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为60°,且满足|$\overrightarrow{a}$-2$\overrightarrow{b}$|=2,则$\overrightarrow{a}$•$\overrightarrow{b}$的最大值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 3 |
5.已知复数z=x+2i(x∈R,i为虚数单位),z2=-3+4i,则x=( )
| A. | ±1 | B. | -1 | C. | 0 | D. | 1 |
15.已知一个几何体的三视图(单位:cm)如图所示,则这个几何体的体积为( )
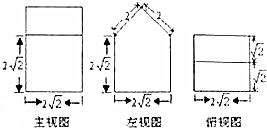

| A. | 16$\sqrt{2}$cm3 | B. | 32$\sqrt{2}$cm3 | C. | 24$\sqrt{2}$cm3 | D. | 20$\sqrt{2}$cm3 |
2.已知复数z=$\frac{1+i}{2-i}$(其中i是虚数单位),则复数z在坐标平面对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
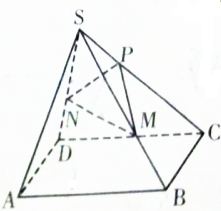 如图,四边形ABCD是正方形,S为四边形ABCD所在平面外一点,SA=SB=SC=SD,P,M,N分别是SC,SB,SD上的点,且PC:SP=SM:MB=SN:ND=2:1,求证:SA∥平面PMN.
如图,四边形ABCD是正方形,S为四边形ABCD所在平面外一点,SA=SB=SC=SD,P,M,N分别是SC,SB,SD上的点,且PC:SP=SM:MB=SN:ND=2:1,求证:SA∥平面PMN.