6.将函数f(x)=$sin(2x-\frac{π}{4})$向右平移$\frac{3π}{8}$个单位,再将所得的函数图象上的各点纵坐标不变,横坐标变为原来的2倍,得到函数y=g(x)的图象,则函数y=g(x)与x=-$\frac{π}{2}$,x=$\frac{π}{3}$,x轴围成的图形面积为( )
| A. | $\frac{5}{2}$ | B. | $1+\frac{{\sqrt{3}}}{2}$ | C. | $\frac{3}{2}$ | D. | $1-\frac{{\sqrt{3}}}{2}$ |
4.直线Ax+By+C=0与圆x2+y2=4相交于两点M、N,若满足C2=A2+B2,则$\overrightarrow{OM}$•$\overrightarrow{ON}$(O为坐标原点)等于( )
| A. | 1 | B. | 0 | C. | -1 | D. | -2 |
3.计算i(1-i)2的值等于( )
| A. | 4 | B. | 2 | C. | -2i | D. | 4i |
20.设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的一条渐近线与抛物线y2=x的一个交点的横坐标为x0,若x0>1,则双曲线C的离心率e的取值范围是( )
| A. | (1,$\frac{\sqrt{6}}{2}$) | B. | ($\sqrt{2}$,+∞) | C. | (1,$\sqrt{2}$) | D. | ($\frac{\sqrt{6}}{2}$,+∞) |
19.点P是曲线y=x2-1nx上任意一点,则点P到直线y=x-2的距离的最小值是( )
0 249932 249940 249946 249950 249956 249958 249962 249968 249970 249976 249982 249986 249988 249992 249998 250000 250006 250010 250012 250016 250018 250022 250024 250026 250027 250028 250030 250031 250032 250034 250036 250040 250042 250046 250048 250052 250058 250060 250066 250070 250072 250076 250082 250088 250090 250096 250100 250102 250108 250112 250118 250126 266669
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
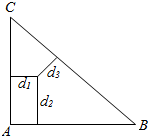 点P在△ABC内部(包含边界),|AC|=3,|AB|=4,|BC|=5,点P到三边的距离分别是d1,d2,d3,则d1+d2+d3的取值范围是[$\frac{12}{5}$,4].
点P在△ABC内部(包含边界),|AC|=3,|AB|=4,|BC|=5,点P到三边的距离分别是d1,d2,d3,则d1+d2+d3的取值范围是[$\frac{12}{5}$,4].