题目内容
1．
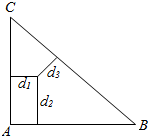点P在△ABC内部（包含边界），|AC|=3，|AB|=4，|BC|=5，点P到三边的距离分别是d1，d2，d3，则d1+d2+d3的取值范围是[$\frac{12}{5}$，4]．
分析 设点P到三边的距离分别是d1，d2，d3，分别为x，y，z，
①由三角形面积公式将△ABC的面积分为三块计算，化简得3x+4y+5z=12，即为x、y、z．所满足的等量关系；
②由①化简出x+y+z=$\frac{12}{5}$+$\frac{1}{5}$（2x+y），设目标函数t=2x+y，并根据不等式画出如图可行域，利用直线平移法解出0≤t≤8，从而可得x+y+z的取值范围，问题得以解决．
解答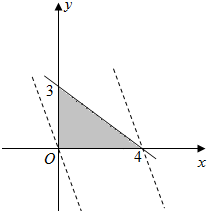 
解：设点P到三边的距离分别是d1，d2，d3，分别令d1=x，d2=y，d3=z，
①S△PAC+S△PBC+S△PAB=S△ABC，可得$\frac{1}{2}$•3x+$\frac{1}{2}$•4y+$\frac{1}{2}$•5z=$\frac{1}{2}$×3×4，故3x+4y+5z=12，
②x+y+z=x+y+$\frac{1}{5}$（12-3x-4y）=$\frac{12}{5}$+$\frac{1}{5}$（2x+y），
令t=2x+y依题意有$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{3x+4y≤12}\end{array}\right.$，
画出可行域如图
可知当x=0，y=0时tmin=0
当x=4，y=0时，tmax=8，即0≤t≤8
故x+y+z=$\frac{12}{5}$+$\frac{1}{5}$t的取值范围为[$\frac{12}{5}$，4]，
故d1+d2+d3的取值范围是[$\frac{12}{5}$，4]，
故答案为：[$\frac{12}{5}$，4]．
点评 本题着重考查了三角形的面积公式，考查了简单的线性规则的知识，请同学们注意解题过程中转化化归、数形结合和方程思想的运用．属于中档题
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
11．已知f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|≤$\frac{π}{2}$）是定义域为R的奇函数，且当x=2时，f（x）取得最大值2，则f（1）+f（2）+f（3）+…+f（100）=（ ）
| A． | 2+2$\sqrt{2}$ | B． | 2-2$\sqrt{2}$ | C． | 2±2$\sqrt{2}$ | D． | 0 |
12．已知函数f（x）=ex-x2，g（x）=ax+b（a＞0），若对?x1∈[0，2]，?x2∈[0，2]，使得f（x1）=g（x2），则实数a，b的取值范围是（ ）
| A． | 0＜a≤$\frac{{{e^2}-5}}{2}$，b≥1 | B． | 0＜a≤$\frac{{{e^2}-5}}{2}$，b≤1 | C． | a≥$\frac{{{e^2}-5}}{2}$，b≥1 | D． | a≥$\frac{{{e^2}-5}}{2}$，b≤1 |
16．在△ABC中，a=$\sqrt{3}$，c=$\sqrt{6}$，B=$\frac{π}{4}$，则b的长为（ ）
| A． | $\sqrt{2}$ | B． | 2$\sqrt{2}$ | C． | $\sqrt{3}$ | D． | 2$\sqrt{3}$ |
6．将函数f（x）=$sin（2x-\frac{π}{4}）$向右平移$\frac{3π}{8}$个单位，再将所得的函数图象上的各点纵坐标不变，横坐标变为原来的2倍，得到函数y=g（x）的图象，则函数y=g（x）与x=-$\frac{π}{2}$，x=$\frac{π}{3}$，x轴围成的图形面积为（ ）
| A． | $\frac{5}{2}$ | B． | $1+\frac{{\sqrt{3}}}{2}$ | C． | $\frac{3}{2}$ | D． | $1-\frac{{\sqrt{3}}}{2}$ |
10．在△ABC中，若$\overrightarrow{CA}•\overrightarrow{CB}=0$，则△ABC是（ ）
| A． | 锐角三角形 | B． | 钝角三角形 | C． | 直角三角形 | D． | 等腰三角形 |