题目内容
6.将函数f(x)=$sin(2x-\frac{π}{4})$向右平移$\frac{3π}{8}$个单位,再将所得的函数图象上的各点纵坐标不变,横坐标变为原来的2倍,得到函数y=g(x)的图象,则函数y=g(x)与x=-$\frac{π}{2}$,x=$\frac{π}{3}$,x轴围成的图形面积为( )| A. | $\frac{5}{2}$ | B. | $1+\frac{{\sqrt{3}}}{2}$ | C. | $\frac{3}{2}$ | D. | $1-\frac{{\sqrt{3}}}{2}$ |
分析 由条件利用函数y=Asin(ωx+φ)的图象变换规律,可得g(x)=-sinx,再利用定积分求得g(x)与x=-$\frac{π}{2}$,x=$\frac{π}{3}$,x轴围成的图形面积.
解答  解:将函数f(x)=$sin(2x-\frac{π}{4})$向右平移$\frac{3π}{8}$个单位,可得y=sin[2(x-$\frac{3π}{8}$)-$\frac{π}{4}$]=-sin(π-2x)=-sin2x的图象;
解:将函数f(x)=$sin(2x-\frac{π}{4})$向右平移$\frac{3π}{8}$个单位,可得y=sin[2(x-$\frac{3π}{8}$)-$\frac{π}{4}$]=-sin(π-2x)=-sin2x的图象;
再将所得的函数图象上的各点纵坐标不变,横坐标变为原来的2倍,得到函数y=g(x)=-sinx的图象,
故函数y=g(x)与x=-$\frac{π}{2}$,x=$\frac{π}{3}$,x轴围成的图形面积为${∫}_{-\frac{π}{2}}^{0}$(-sinx)-${∫}_{0}^{\frac{π}{3}}$(-sinx)=${|}_{-\frac{π}{2}}^{0}$cosx-${|}_{0}^{\frac{π}{3}}$(cosx)=1+$\frac{1}{2}$=$\frac{3}{2}$,
故选:C.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,用定积分求曲线围成的面积,属于中档题.

练习册系列答案
相关题目
11.设函数f(x)=loga|x+b|在定义域内具有奇偶性,f(b-2)与f(a+1)的大小关系是( )
| A. | f(b-2)=f(a+1) | B. | f(b-2)>f(a+1) | C. | f(b-2)<f(a+1) | D. | 不能确定 |
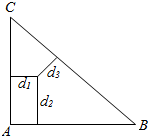 点P在△ABC内部(包含边界),|AC|=3,|AB|=4,|BC|=5,点P到三边的距离分别是d1,d2,d3,则d1+d2+d3的取值范围是[$\frac{12}{5}$,4].
点P在△ABC内部(包含边界),|AC|=3,|AB|=4,|BC|=5,点P到三边的距离分别是d1,d2,d3,则d1+d2+d3的取值范围是[$\frac{12}{5}$,4].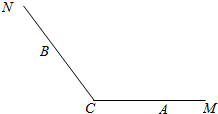 已知点A,B分别在射线CM,CN(不含端点C)上运动,∠MCN=$\frac{2π}{3}$,在△ABC中,角A,B,C所对的边分别是a,b,c
已知点A,B分别在射线CM,CN(不含端点C)上运动,∠MCN=$\frac{2π}{3}$,在△ABC中,角A,B,C所对的边分别是a,b,c