题目内容
19.点P是曲线y=x2-1nx上任意一点,则点P到直线y=x-2的距离的最小值是( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
分析 画出函数的图象,故当点P是曲线的切线中与直线y=x-2平行的直线的切点时,然后求解即可.
解答 解:由题意作图如下,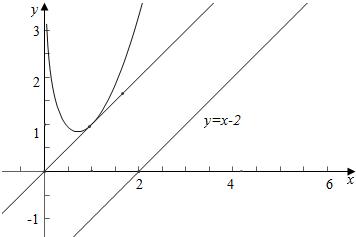
当点P是曲线的切线中与直线y=x-2平行的直线的切点时,最近;
故令y′=2x-$\frac{1}{x}$=1解得,x=1;
故点P的坐标为(1,1);
故点P到直线y=x-2的最小值为$\frac{|1-2-1|}{\sqrt{1+1}}$=$\sqrt{2}$;
故选:B.
点评 本题考查了几何意义的运用及导数的综合应用,平行线之间距离的求法,考查转化思想以及计算能力,属于中档题.

练习册系列答案
相关题目
9.已知非常数列且各项为正数等比数列{an}中,则( )
| A. | a1+a2014>a1007+a1008 | B. | a1+a2014<a1007+a1008 | ||
| C. | a1+a2014≥a1007+a1008 | D. | a1+a2014与a1007+a1008无法比较 |
10.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>b>0)的右顶点为A,若该双曲线右支上存在两点B,C使得△ABC为等腰直角三角形,则该双曲线的离心率e的取值范围是( )
| A. | (1,3) | B. | ($1,\sqrt{3}$) | C. | (1,2) | D. | ($1,\sqrt{2}$) |
7.设f(x)=xsinx,x∈$[{-\frac{π}{2},\frac{π}{2}}]$,若f(x1)>f(x2),则下列不等式中必定成立的是( )
| A. | x1-x2<0 | B. | x1-x2>0 | C. | x12-x22>0 | D. | x12<x22 |
4.直线Ax+By+C=0与圆x2+y2=4相交于两点M、N,若满足C2=A2+B2,则$\overrightarrow{OM}$•$\overrightarrow{ON}$(O为坐标原点)等于( )
| A. | 1 | B. | 0 | C. | -1 | D. | -2 |
11.设函数f(x)=loga|x+b|在定义域内具有奇偶性,f(b-2)与f(a+1)的大小关系是( )
| A. | f(b-2)=f(a+1) | B. | f(b-2)>f(a+1) | C. | f(b-2)<f(a+1) | D. | 不能确定 |
8.扇形的半径是6cm,圆心角为15°,则扇形面积是( )
| A. | $\frac{π}{2}c{m^2}$ | B. | 3πcm2 | C. | πcm2 | D. | $\frac{3π}{2}c{m^2}$ |