11.设P是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)上一点,F1(-c,0),F2(c,0)(c>0)为左、右焦点,△PF1F2周长为6c,面积为$\frac{2\sqrt{3}}{3}$a2,则双曲线的离心率是( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 3 |
10.已知抛物线x2=2py(p>0)的焦点与双曲线x2-y2=-$\frac{1}{2}$的一个焦点重合,且在抛物线上有一动点P到x轴的距离为m,P到直线l:2x-y-4=0的距离为n,则m+n的最小值为( )
0 249763 249771 249777 249781 249787 249789 249793 249799 249801 249807 249813 249817 249819 249823 249829 249831 249837 249841 249843 249847 249849 249853 249855 249857 249858 249859 249861 249862 249863 249865 249867 249871 249873 249877 249879 249883 249889 249891 249897 249901 249903 249907 249913 249919 249921 249927 249931 249933 249939 249943 249949 249957 266669
| A. | $\sqrt{5}$+1 | B. | $\sqrt{5}$-1 | C. | $\sqrt{5}$ | D. | 2$\sqrt{5}$-2 |
 如图,平面AEFD⊥平面BCFE,其中AEFD为正方形,BCFE为直角梯形,BE∥CF,BE⊥EF,BE=EF=$\frac{1}{2}$CF=1.
如图,平面AEFD⊥平面BCFE,其中AEFD为正方形,BCFE为直角梯形,BE∥CF,BE⊥EF,BE=EF=$\frac{1}{2}$CF=1.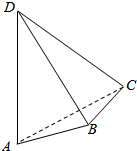 如图,AD与BC是四面体ABCD中互相垂直的棱,若BC=2,AD=4,且∠ABD=∠ACD=60°,则四面体ABCD的体积的最大值是$\frac{4}{3}\sqrt{11}$.
如图,AD与BC是四面体ABCD中互相垂直的棱,若BC=2,AD=4,且∠ABD=∠ACD=60°,则四面体ABCD的体积的最大值是$\frac{4}{3}\sqrt{11}$.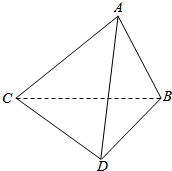 如图,在△ABC中,AB=AC,∠BAC=90°,△BCD中,∠CBD=90°,∠BDC=60°,BC=6,△ABC和△BCD相互垂直.
如图,在△ABC中,AB=AC,∠BAC=90°,△BCD中,∠CBD=90°,∠BDC=60°,BC=6,△ABC和△BCD相互垂直.