题目内容
10.已知抛物线x2=2py(p>0)的焦点与双曲线x2-y2=-$\frac{1}{2}$的一个焦点重合,且在抛物线上有一动点P到x轴的距离为m,P到直线l:2x-y-4=0的距离为n,则m+n的最小值为( )| A. | $\sqrt{5}$+1 | B. | $\sqrt{5}$-1 | C. | $\sqrt{5}$ | D. | 2$\sqrt{5}$-2 |
分析 求得双曲线的一个焦点,可得p=2,求得抛物线的准线方程,运用抛物线的定义,结合三点共线,由点到直线的距离公式,计算即可得到最小值.
解答 解:由双曲线x2-y2=-$\frac{1}{2}$的一个焦点为(0,1),
则抛物线x2=2py(p>0)的焦点为(0,1),即有p=2,
则抛物线的方程为x2=4y,准线为x=-1,
由抛物线的定义,可得m=|PF|-1,
设|PH|=n,(H为P到直线l所作垂线的垂足),
因此m+n=|PF|-1+|PH|.
易知当F,P,H三点共线时,m+n最小,
因此其最小值为|FH|-1=$\frac{|-1-4|}{\sqrt{5}}$-1=$\sqrt{5}$-1.
故选:B.
点评 本题考查双曲线和抛物线的定义、方程和性质,考查三点共线取得最小的运用,属于中档题.

练习册系列答案
 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
11.将一根长度为a(a为正常数)的合金做成“田”字形窗户.当窗户的面积最大时,窗户的长宽之比为 ( )
| A. | $\sqrt{2}$:1 | B. | $\sqrt{3}$:$\sqrt{2}$ | C. | 1:1 | D. | 2:1 |
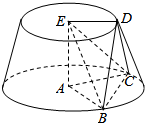 如图圆台的上下底面的圆心分别是E、A,点D在上底面圆周上,B、C在下底面圆周上,已知EA=1,ED=$\sqrt{3}$,AC=BC=2,BD=CD.
如图圆台的上下底面的圆心分别是E、A,点D在上底面圆周上,B、C在下底面圆周上,已知EA=1,ED=$\sqrt{3}$,AC=BC=2,BD=CD.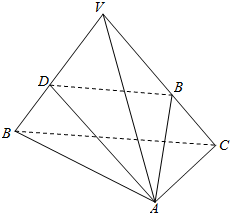 设正三棱锥V-ABC的底面边长为4,侧棱长为8,过A作与侧棱VB,VC相交的截面AED,求截面三角形AED的周长的最小值.
设正三棱锥V-ABC的底面边长为4,侧棱长为8,过A作与侧棱VB,VC相交的截面AED,求截面三角形AED的周长的最小值. 在四棱锥C-ABDE中,F为CD的中点,DB⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE.
在四棱锥C-ABDE中,F为CD的中点,DB⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE.