题目内容
3.已知a∥b,a⊥α,b⊥β,求证:α∥β.
分析 通过在平面α内作两条相交直线m、n,利用直线与平面垂直的定义及a⊥α可知a⊥m、a⊥n,通过a∥b可知b⊥m、b⊥n,利用线面垂直的判定定理可知b⊥α,结合b⊥β即得结论.
解答 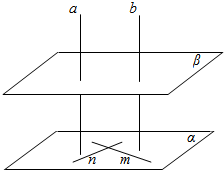 证明:在平面α内作两条相交直线m、n,
证明:在平面α内作两条相交直线m、n,
∵直线a⊥平面α,及直线与平面垂直的定义,
∴a⊥m、a⊥n,
又∵a∥b,
∴b⊥m、b⊥n,
又∵m?α、n?α,m、n相交,
∴b⊥α,
又∵b⊥β,
∴α∥β.
点评 本题考查平面垂直的性质及判定、面面平行的判定,注意解题方法的积累,属于基础题.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
14.已知正方体ABCD-A1B1C1D1的棱长为a,定点M在棱AB上(不在端点A、B上),点P是平面ABCD内的动点,且点P到直线A1D1的距离与点P到点M的距离的平方差为a2,则点P的轨迹所在曲线为( )
| A. | 抛物线 | B. | 双曲线 | C. | 直线 | D. | 圆 |
12.某地区汽车限行规定如下:
某地区某行政单位有车牌尾号为6的汽车A和尾号为9的汽车B,在非限行日,A车日出车频率为p,B车日出车频率为q,周六、周日和限行日停止用车,现将汽车日出车频率视为日出车概率,且A,B两车是否出车相互独立.
(1)若p=0.8,求汽车A在同一周内恰有两天连续出车的概率;
(2)若p∈[0.4,0.8],且两车的日出车频率之和为1,为实现节能减排与绿色出行,应如何调控两车的日出车频率,使得一周内汽车A,B同日都出车的平均天数最少.
| 车尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
| 限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
(1)若p=0.8,求汽车A在同一周内恰有两天连续出车的概率;
(2)若p∈[0.4,0.8],且两车的日出车频率之和为1,为实现节能减排与绿色出行,应如何调控两车的日出车频率,使得一周内汽车A,B同日都出车的平均天数最少.
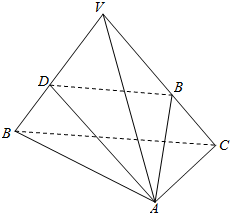 设正三棱锥V-ABC的底面边长为4,侧棱长为8,过A作与侧棱VB,VC相交的截面AED,求截面三角形AED的周长的最小值.
设正三棱锥V-ABC的底面边长为4,侧棱长为8,过A作与侧棱VB,VC相交的截面AED,求截面三角形AED的周长的最小值.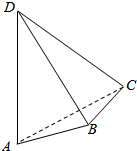 如图,AD与BC是四面体ABCD中互相垂直的棱,若BC=2,AD=4,且∠ABD=∠ACD=60°,则四面体ABCD的体积的最大值是$\frac{4}{3}\sqrt{11}$.
如图,AD与BC是四面体ABCD中互相垂直的棱,若BC=2,AD=4,且∠ABD=∠ACD=60°,则四面体ABCD的体积的最大值是$\frac{4}{3}\sqrt{11}$.