题目内容
7.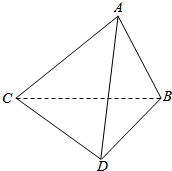 如图,在△ABC中,AB=AC,∠BAC=90°,△BCD中,∠CBD=90°,∠BDC=60°,BC=6,△ABC和△BCD相互垂直.
如图,在△ABC中,AB=AC,∠BAC=90°,△BCD中,∠CBD=90°,∠BDC=60°,BC=6,△ABC和△BCD相互垂直.(1)求证:平面ABD⊥平面ACD.
(2)求二面角A-CD-B的正切值.
分析 (1)如图所示,取BC的中点O,CD的中点M,连接OA,OM.可得AO⊥BC.利用面面垂直的性质定理可得:AO⊥平面BCD,AO⊥OM.又OM∥BD,BD⊥BC,可得OM⊥BC.
以OM,OB,OA所在直线建立空间直角坐标系.利用线面垂直的性质定理分别求出平面ACD的法向量为$\overrightarrow{m}$,平面ABD的法向量$\overrightarrow{n}$.只要证明$\overrightarrow{m}•\overrightarrow{n}$=0,即可.
(2)取平面ACB的法向量$\overrightarrow{v}$=(1,0,0).可得$cos<\overrightarrow{m},\overrightarrow{v}>$=$\frac{\overrightarrow{m}•\overrightarrow{v}}{|\overrightarrow{m}||\overrightarrow{v}|}$.再利用同角三角函数基本关系式即可得出.
解答 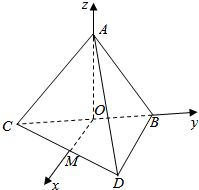 (1)证明:如图所示,
(1)证明:如图所示,
取BC的中点O,CD的中点M,连接OA,OM.
又∵AC=AB,∴AO⊥BC,
∵平面ABC⊥平面BCD,
∴AO⊥平面BCD.
∴AO⊥OM.
∵OM∥BD,BD⊥BC,
∴OM⊥BC.
以OM,OB,OA所在直线建立空间直角坐标系.
则A(0,0,3),B(0,3,0),C(0,-3,0),D(2$\sqrt{3}$,3,0).
∴$\overrightarrow{AD}$=(2$\sqrt{3}$,3,-3),$\overrightarrow{AC}$=(0,-3,-3),$\overrightarrow{AB}$=(0,3,-3).
设平面ACD的法向量为$\overrightarrow{m}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AD}=0}\\{\overrightarrow{m}•\overrightarrow{AC}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{2\sqrt{3}x+3y-3z=0}\\{-3y-3z=0}\end{array}\right.$,
取$\overrightarrow{m}$=$(\sqrt{3},-1,1)$.
同理可得平面ABD的法向量$\overrightarrow{n}$=(0,1,1).
∵$\overrightarrow{m}•\overrightarrow{n}$=0-1+1=0,
∴$\overrightarrow{m}⊥\overrightarrow{n}$.
∴平面ABD⊥平面ACD.
(2)解:取平面ACB的法向量$\overrightarrow{v}$=(1,0,0).
则$cos<\overrightarrow{m},\overrightarrow{v}>$=$\frac{\overrightarrow{m}•\overrightarrow{v}}{|\overrightarrow{m}||\overrightarrow{v}|}$=$\frac{\sqrt{3}}{\sqrt{5}×1}$=$\frac{\sqrt{15}}{5}$.
∴$sin<\overrightarrow{m},\overrightarrow{v}>$=$\sqrt{1-(\frac{\sqrt{15}}{5})^{2}}$=$\frac{\sqrt{10}}{5}$.
∴二面角A-CD-B的正切值=$\frac{sin<\overrightarrow{m},\overrightarrow{v}>}{cos<\overrightarrow{m},\overrightarrow{v}>}$=$\frac{\frac{\sqrt{10}}{5}}{\frac{\sqrt{15}}{5}}$=$\frac{\sqrt{6}}{3}$.
点评 本题考查了空间线面位置关系、空间角、同角三角函数基本关系式,考查了推理能力与计算能力,属于中档题.

 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
 如图,平面EFGH分别平行于CD,AB,点E,F,G,H分别在AC,AD,BD,BC上,且CD=a,AB=b,CD⊥AB.
如图,平面EFGH分别平行于CD,AB,点E,F,G,H分别在AC,AD,BD,BC上,且CD=a,AB=b,CD⊥AB.