16．淘宝卖家在某商品的所有买家中，随机选择男女买家各50名进行调查，他们的评分等级如下表：
（1）从评分等级为（4，5]的人中随机选取两人，求恰有一人是男性的概率；
（2）规定：评分等级在[0，3]内为不满意该商品，在（3，5]内为满意该商品．完成下列2×2列联表并帮助卖家判断：能否在犯错误的概率不超过0.05的前提下认为满意该商品与性别有关系？
参考数据：
（参考公式：K2=$\frac{n（ad-c）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
| 评分等级 | [0，1] | （1，2] | （2，3] | （3，4] | （4，5] |
| 女（人数） | 2 | 7 | 9 | 20 | 12 |
| 男（人数） | 3 | 9 | 18 | 12 | 8 |
（2）规定：评分等级在[0，3]内为不满意该商品，在（3，5]内为满意该商品．完成下列2×2列联表并帮助卖家判断：能否在犯错误的概率不超过0.05的前提下认为满意该商品与性别有关系？
| 满意该商品 | 不满意该商品 | 总计 | |
| 女 | |||
| 男 | |||
| 总计 |
| P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
15．已知函数f（x）=-x3+ax2-x-1在（-∞，+∞）上是单调函数，则实数a的取值范围是（ ）
| A． | [-$\sqrt{3}$，$\sqrt{3}$] | B． | （-$\sqrt{3}$，$\sqrt{3}$） | C． | （-∞，-$\sqrt{3}$）∪（$\sqrt{3}$，+∞） | D． | （-∞，-$\sqrt{3}$）∩（$\sqrt{3}$，+∞） |
13．某校举行运动会，组委会招募了16名男志愿者和14名女志愿者，调查发现，男、女志愿者中分别有10 人和6人喜爱运动，其余不喜爱．
（Ⅰ）根据以上数据完成以下2×2列联表：
（Ⅱ）根据列联表的独立性检验，有多大的把握认为性别与喜爱运动有关？
（Ⅲ）从不喜爱运动的女志愿者中和喜爱运动的女志愿者中各选1人，求其中不喜爱运动的女生甲及喜爱运动的女生乙至少有一人被选取的概率．
参考公式：${Χ^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（b+c）（a+c）（b+d）}$（其中n=a+b+c+d）
注：Χ2≤2.706，就认为没有充分证据显示“性别与喜爱运动有关”；Χ2＞2.706，就有90%的把握认为“性别与喜爱运动有关”；Χ2＞3.841，就有95%的把握认为“性别与喜爱运动有关”．
（Ⅰ）根据以上数据完成以下2×2列联表：
| 喜爱运动 | 不喜爱运动 | 总计 | |
| 男 | 10 | 16 | |
| 女 | 6 | 14 | |
| 总计 | 30 |
（Ⅲ）从不喜爱运动的女志愿者中和喜爱运动的女志愿者中各选1人，求其中不喜爱运动的女生甲及喜爱运动的女生乙至少有一人被选取的概率．
参考公式：${Χ^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（b+c）（a+c）（b+d）}$（其中n=a+b+c+d）
注：Χ2≤2.706，就认为没有充分证据显示“性别与喜爱运动有关”；Χ2＞2.706，就有90%的把握认为“性别与喜爱运动有关”；Χ2＞3.841，就有95%的把握认为“性别与喜爱运动有关”．
12．在△ABC中，$\overrightarrow{BD}$=$\frac{3}{4}$$\overrightarrow{BC}$，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，则向量$\overrightarrow{AD}$=（ ）
| A． | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{3}{4}$$\overrightarrow{b}$ | B． | $\frac{3}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ | C． | $\frac{7}{4}$$\overrightarrow{a}$-$\frac{3}{4}$$\overrightarrow{b}$ | D． | -$\frac{7}{4}$$\overrightarrow{a}$+$\frac{3}{4}$$\overrightarrow{b}$ |
11．已知向量$\overrightarrow{a}$=（-1，2），$\overrightarrow{b}$=（2，x），若$\overrightarrow{a}$⊥$\overrightarrow{b}$，则实数x等于（ ）
| A． | 1 | B． | -1 | C． | -4 | D． | 4 |
9．
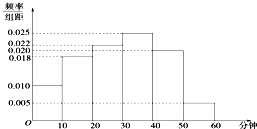电视传媒公司为了解某地区观众对某体育节目的收视情况，随机抽取了100名观众进行调查，其中女性有55名，下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图：
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”．
（1）根据已知条件完成下面的2×2列联表，并据此资料你是否认为“体育迷”与性别有关？
附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．
（2）将上述调查所得到的频率视为概率．现在从该地区大量电视观众中，采用随机抽样方法每次抽取1名观众，抽取3次，记被抽取的3名观众中的“体育迷”人数为X．若每次抽取的结果是相互独立的，求X的分布列，期望E（X）和方差D（X）．
电视传媒公司为了解某地区观众对某体育节目的收视情况，随机抽取了100名观众进行调查，其中女性有55名，下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图：将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”．
（1）根据已知条件完成下面的2×2列联表，并据此资料你是否认为“体育迷”与性别有关？
| 非体育迷 | 体育迷 | 合计 | |
| 男 | |||
| 女 | 10 | 55 | |
| 合计 |
| P（K2≥k） | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
8．函数f（x）=$\left\{\begin{array}{l}{1，x为有理数}\\{0，x为无理数}\end{array}\right.$则f（f（$\sqrt{2}$））等于（ ）
0 248002 248010 248016 248020 248026 248028 248032 248038 248040 248046 248052 248056 248058 248062 248068 248070 248076 248080 248082 248086 248088 248092 248094 248096 248097 248098 248100 248101 248102 248104 248106 248110 248112 248116 248118 248122 248128 248130 248136 248140 248142 248146 248152 248158 248160 248166 248170 248172 248178 248182 248188 248196 266669
| A． | 0 | B． | 1 | C． | $\sqrt{2}$ | D． | $1+\sqrt{2}$ |