题目内容
10.若复数z=$\frac{a+3i}{1-2i}$(a∈R),且z是纯虚数,则|a+2i|等于2$\sqrt{10}$.分析 化简已知复数,由纯虚数的定义可得a值,再由复数的模长公式可得.
解答 解:化简可得z=$\frac{a+3i}{1-2i}$=$\frac{(a+3i)(1+2i)}{(1-2i)(1+2i)}$
=$\frac{a+2ai+3i+6{i}^{2}}{1-4{i}^{2}}$=$\frac{a-6+(2a+3)i}{5}$,
∵z是纯虚数,∴a-6=0且2a+3≠0,解得a=6,
∴|a+2i|=|6+2i|=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$
故答案为:2$\sqrt{10}$
点评 本题考查复数的代数形式的乘除运算,涉及复数的模长公式,属基础题.

练习册系列答案
相关题目
18.设随机变量ξ服从正态分布N(0,1),P(ξ>1)=P,则P(-1<ξ<O)=( )
| A. | $\frac{1}{2}$P | B. | $\frac{1}{2}$-P | C. | 1-2P | D. | 1-P |
5.以下命题正确的个数是( )
①命题“?x∈R,sinx>0”的否定是“?x∈R,sinx<0”.
②命题“若x2+x-12=0,则x=4”的逆否命题为“若x≠4,则x2+x-12≠0”.
③若p∧q为假命题,则p、q均为假命题.
①命题“?x∈R,sinx>0”的否定是“?x∈R,sinx<0”.
②命题“若x2+x-12=0,则x=4”的逆否命题为“若x≠4,则x2+x-12≠0”.
③若p∧q为假命题,则p、q均为假命题.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
15.已知函数f(x)=-x3+ax2-x-1在(-∞,+∞)上是单调函数,则实数a的取值范围是( )
| A. | [-$\sqrt{3}$,$\sqrt{3}$] | B. | (-$\sqrt{3}$,$\sqrt{3}$) | C. | (-∞,-$\sqrt{3}$)∪($\sqrt{3}$,+∞) | D. | (-∞,-$\sqrt{3}$)∩($\sqrt{3}$,+∞) |
2.如果(2x-y)+(x+3)i=0(x,y∈R),则x+y的值是( )
| A. | 18 | B. | $\frac{1}{2}$ | C. | 3 | D. | -9 |
17.$\frac{1}{2}+({\frac{1}{2}+\frac{1}{4}})+({\frac{1}{2}+\frac{1}{4}+\frac{1}{8}})+…+({\frac{1}{2}+\frac{1}{4}+…+\frac{1}{{{2^{10}}}}})$的值为( )
| A. | 7+$\frac{1}{2^9}$ | B. | 9+$\frac{1}{{{2^{10}}}}$ | C. | 11+$\frac{1}{{{2^{11}}}}$ | D. | 7+$\frac{1}{{{2^{10}}}}$ |
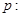 关于
关于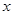 的方程
的方程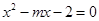 在
在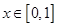 有解,命题
有解,命题 在
在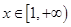 单调递增;若
单调递增;若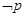 为真命题,
为真命题,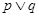 是真命题,求实数
是真命题,求实数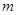 的取值范围.
的取值范围.