8.某饮料销售点销售某品牌饮料,饮料的零售价x(元/瓶)与销量y(瓶)的关系统计如下:
由表中数据得线性回归方程:$\widehat{y}$=-20x+a,当零售价为每瓶3.7元时,估计该销售点销售的这种饮料的瓶数为( )
| 零售价x(元/瓶) | 3.0 | 3.2 | 3.4 | 3.6 | 3.8 | 4.0 |
| 销量y(瓶) | 50 | 44 | 43 | 40 | 35 | 28 |
| A. | 39 | B. | 38 | C. | 37 | D. | 36 |
7.用反证法证明命题:“三个连续正整数a,b,c中至少有一个能被2整除”时,要做的假设是( )
| A. | 假设三个连续正整数a,b,c都不能被2整除 | |
| B. | 假设三个连续正整数a,b,c都能被2整除 | |
| C. | 假设三个连续正整数a,b,c至多有一个能被2整除 | |
| D. | 假设三个连续正整数a,b,c至多有两个能被2整除 |
5.若动点P在直线l1:x-y-2=0上,动点Q在直线l2:x-y-6=0上,设线段PQ的中点M(a,b),满足a2+b2-4a+4b≤0,则a2+b2的取值范围是( )
| A. | [2$\sqrt{2}$,4] | B. | [2$\sqrt{2}$,2$\sqrt{3}$] | C. | [8,12] | D. | [8,16] |
3.若$α∈(2kπ+\frac{π}{4},2kπ+\frac{π}{2})$(k∈Z),则sinα,cosα,tanα的大小关系为( )
0 247874 247882 247888 247892 247898 247900 247904 247910 247912 247918 247924 247928 247930 247934 247940 247942 247948 247952 247954 247958 247960 247964 247966 247968 247969 247970 247972 247973 247974 247976 247978 247982 247984 247988 247990 247994 248000 248002 248008 248012 248014 248018 248024 248030 248032 248038 248042 248044 248050 248054 248060 248068 266669
| A. | tanα>sinα>cosα | B. | tanα>cosα>sinα | C. | tanα<sinα<cosα | D. | tanα<cosα<sinα |
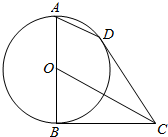 如图所示,AB为圆O的直径,BC,CD为圆O的切线,B,D为切点.
如图所示,AB为圆O的直径,BC,CD为圆O的切线,B,D为切点.