13.变量x与变量y有如下对应关系
则其线性回归直线必过定点(4,5).
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
11.已知点A(3,4)和B(0,8),则|AB|=( )
| A. | 25 | B. | 5 | C. | $\sqrt{7}$ | D. | 7 |
10. 某研究机构对高三学生的记忆力x和判断力y进行统计分析,所得数据如表所示:
某研究机构对高三学生的记忆力x和判断力y进行统计分析,所得数据如表所示:
(1)在给定的坐标系中画出表中数据的散点图;
(2)试根据最小二乘法原理,求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,并在给定的坐标系中画出回归直线;
(3)试根据(2)求出的线性回归方程,预测记忆力为9的学生的判断力.
参考公式:用最小二乘法求线性回归方程系数公式:$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}},\hat a=\overline y-\hat b\overline x$.
 某研究机构对高三学生的记忆力x和判断力y进行统计分析,所得数据如表所示:
某研究机构对高三学生的记忆力x和判断力y进行统计分析,所得数据如表所示:| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
(2)试根据最小二乘法原理,求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,并在给定的坐标系中画出回归直线;
(3)试根据(2)求出的线性回归方程,预测记忆力为9的学生的判断力.
参考公式:用最小二乘法求线性回归方程系数公式:$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}},\hat a=\overline y-\hat b\overline x$.
9. 生物兴趣小组的同学到野外调查某种植物的生长情况,共测量了k∈Z株该植物的高度(单位:厘米),获得数据如下:
生物兴趣小组的同学到野外调查某种植物的生长情况,共测量了k∈Z株该植物的高度(单位:厘米),获得数据如下:
6,7,8,9,10,14,16,17,17,18,19,20,20,21,24,26,26,27,28,29,29,30,30,30,31,31,33,36,37,41.
根据上述数据得到样本的频率分布表如下:
(1)确定样本频率分布表中n1,n2,f1和f2的值;
(2)根据上述频率分布表,画出样本频率分布直方图;
(3)用(2)的频率分布直方图估计该植物生长高度的平均值.
0 247529 247537 247543 247547 247553 247555 247559 247565 247567 247573 247579 247583 247585 247589 247595 247597 247603 247607 247609 247613 247615 247619 247621 247623 247624 247625 247627 247628 247629 247631 247633 247637 247639 247643 247645 247649 247655 247657 247663 247667 247669 247673 247679 247685 247687 247693 247697 247699 247705 247709 247715 247723 266669
 生物兴趣小组的同学到野外调查某种植物的生长情况,共测量了k∈Z株该植物的高度(单位:厘米),获得数据如下:
生物兴趣小组的同学到野外调查某种植物的生长情况,共测量了k∈Z株该植物的高度(单位:厘米),获得数据如下:6,7,8,9,10,14,16,17,17,18,19,20,20,21,24,26,26,27,28,29,29,30,30,30,31,31,33,36,37,41.
根据上述数据得到样本的频率分布表如下:
| 分组 | 频数 | 频率 |
| [5,15] | 6 | 0.2 |
| (15,25] | 9 | 0.3 |
| (25,35] | n1 | f1 |
| (35,45] | n2 | f2 |
(2)根据上述频率分布表,画出样本频率分布直方图;
(3)用(2)的频率分布直方图估计该植物生长高度的平均值.
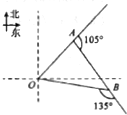 如图,一只蜘蛛从点O出发沿北偏东45°方向爬行xcm,到达点A处捕捉到一只小虫,然后沿OA方向右转105°爬行10cm,到达点B处捕捉哦另一只小虫,这时他沿AB方向右转135°爬行回到它的出发点O处,那么x=$\frac{10\sqrt{6}}{3}$.
如图,一只蜘蛛从点O出发沿北偏东45°方向爬行xcm,到达点A处捕捉到一只小虫,然后沿OA方向右转105°爬行10cm,到达点B处捕捉哦另一只小虫,这时他沿AB方向右转135°爬行回到它的出发点O处,那么x=$\frac{10\sqrt{6}}{3}$.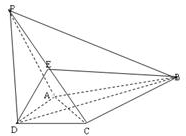 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.