20.双曲线$\frac{x^2}{3}-\frac{y^2}{2}=1$的焦距为( )
| A. | $3\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $2\sqrt{5}$ | D. | $4\sqrt{5}$ |
19.已知抛物线$y=\frac{1}{8}{x^2}$与双曲线$\frac{y^2}{a^2}-{x^2}=1(a>0)$有共同的焦点F,O为坐标原点,P在x轴上方且在双曲线上,则$\overrightarrow{OP}•\overrightarrow{FP}$的最小值为( )
| A. | $3-2\sqrt{3}$ | B. | $2\sqrt{3}-3$ | C. | $-\frac{7}{4}$ | D. | $\frac{3}{4}$ |
18.△ABC中,角A,B,C所对的边分别为a,b,c,若a=$\sqrt{7}$,b=3,c=2,则∠A=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
17.已知函数f(x)=2sin(ωx+φ)$({ω>0,|φ|<\frac{π}{2}})$的图象如图所示,则函数f(x)的解析式是( )
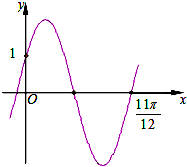

| A. | $f(x)=2sin({\frac{10}{11}x+\frac{π}{6}\;})$ | B. | $f(x)=2sin({\frac{10}{11}x-\frac{π}{6}\;})$ | ||
| C. | $f(x)=2sin({2x+\frac{π}{6}\;})$ | D. | $f(x)=2sin({2x-\frac{π}{6}\;})$ |
15.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2.若双曲线C上存在一点P,使得△PF1F2为等腰三角形,且cos∠PF1F2=$\frac{1}{8}$,则双曲线的离心率为( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
14.设F1,F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的两个焦点,P在双曲线上,若$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0$,$|{\overrightarrow{P{F_1}}}|•|{\overrightarrow{P{F_2}}}|=2ac$(c为半焦距),则双曲线的离心率为( )
| A. | $\frac{{\sqrt{3}-1}}{2}$ | B. | $\frac{{\sqrt{3}+1}}{2}$ | C. | 2 | D. | $\frac{{\sqrt{5}+1}}{2}$ |
12.使cosx=1-m有意义的m的取值范围为( )
0 247441 247449 247455 247459 247465 247467 247471 247477 247479 247485 247491 247495 247497 247501 247507 247509 247515 247519 247521 247525 247527 247531 247533 247535 247536 247537 247539 247540 247541 247543 247545 247549 247551 247555 247557 247561 247567 247569 247575 247579 247581 247585 247591 247597 247599 247605 247609 247611 247617 247621 247627 247635 266669
| A. | m≥0 | B. | 0≤m≤2 | C. | -1<m<1 | D. | m<-1或m>1 |
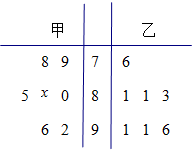 某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.
某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.