1.有5名游客到公园坐游艇,分别坐甲、乙两个游艇,每个游艇至少安排2名游客,那么互不相同的安排方法的种数为( )
| A. | 10 | B. | 20 | C. | 30 | D. | 40 |
15.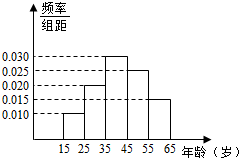 某电视台为宣传海南,随机对海南15~65岁的人群抽取了n人,回答问题“东环铁路沿线有哪几个城市?”统计结果如图表所示:
某电视台为宣传海南,随机对海南15~65岁的人群抽取了n人,回答问题“东环铁路沿线有哪几个城市?”统计结果如图表所示:
(1)分别求出a,b,x,y的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.
 某电视台为宣传海南,随机对海南15~65岁的人群抽取了n人,回答问题“东环铁路沿线有哪几个城市?”统计结果如图表所示:
某电视台为宣传海南,随机对海南15~65岁的人群抽取了n人,回答问题“东环铁路沿线有哪几个城市?”统计结果如图表所示:| 组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
| 第1组 | [15,25) | a | 0.5 |
| 第2组 | [25,35) | 18 | x |
| 第3组 | [35,45) | b | 0.9 |
| 第4组 | [45,55) | 9 | 0.36 |
| 第5组 | [55,65) | 3 | y |
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.
13.为研究某市高中教育投资情况,现将该市某高中学校的连续5年的教育投资数据进行统计,已知年编号x与对应教育投资y(单位:百万元)的抽样数据如下表:
(1)求y关于x的线性回归方程;
(2)利用(1)中的回归方程,分析5年来的该高中教育投资变化情况,预测该高中下一年的教育投资约为多少?
附:回归直线的斜率和截距的最小二乘估计公式分别为:
(参考公式:回归直线方程式$\hat y=\hat bx+\hat a$,其中$\hat b=\frac{{\sum_{i=1}^n{({x_i}-\bar x)({y_i}-\bar y})}}{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}},\hat a=\bar y-\hat b\bar x$)
| 单位编号x | 1 | 2 | 3 | 4 | 5 |
| 投资额y | 3.3 | 3.6 | 3.9 | 4.4 | 4.8 |
(2)利用(1)中的回归方程,分析5年来的该高中教育投资变化情况,预测该高中下一年的教育投资约为多少?
附:回归直线的斜率和截距的最小二乘估计公式分别为:
(参考公式:回归直线方程式$\hat y=\hat bx+\hat a$,其中$\hat b=\frac{{\sum_{i=1}^n{({x_i}-\bar x)({y_i}-\bar y})}}{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}},\hat a=\bar y-\hat b\bar x$)
12.一个袋内装有大小相同的6个白球和5个黑球,从中随意抽取2个球,抽到白球、黑球各1个的概率为( )
0 247425 247433 247439 247443 247449 247451 247455 247461 247463 247469 247475 247479 247481 247485 247491 247493 247499 247503 247505 247509 247511 247515 247517 247519 247520 247521 247523 247524 247525 247527 247529 247533 247535 247539 247541 247545 247551 247553 247559 247563 247565 247569 247575 247581 247583 247589 247593 247595 247601 247605 247611 247619 266669
| A. | $\frac{6}{11}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{11}$ | D. | $\frac{1}{10}$ |
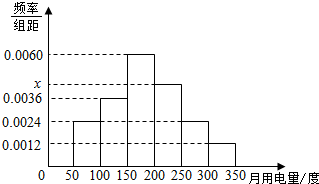 为调查我校学生的用电情况,学校后勤部门组织抽取了100间学生宿舍某月用电量调查,发现每间宿舍用电量都在50度到350度之间,其频率分布直方图如图所示.
为调查我校学生的用电情况,学校后勤部门组织抽取了100间学生宿舍某月用电量调查,发现每间宿舍用电量都在50度到350度之间,其频率分布直方图如图所示.