题目内容
20．在一张节目表中，原有6个节目，如果保持这些节目的相对顺序不变，再添加进去两个节目，求共有56种安排方法．分析 6个节目可产生7个空位，第一个节目可插入到其中的任何一个位置，第一个节目插入后，7个节目会产生8个空位，第二个节目可插入其一，由乘法原理即可解决问题．
解答 解：∵6个节目可产生7个空位，保持这些节目的相对顺序不变，第一个节目可插入到其中的任何一个位置，有C71种方法，
当第一个节目插入后，7个节目会产生8个空位，第二个节目可插入其一，仍然保持这些节目的相对顺序不变，有C81种方法，
根据乘法原理，不同的节目表可排出C71•C81=56种．
故答案为：56．
点评 本题考查排列、组合及简单计数问题，关键是对题意的正确理解及分步计数原理的正确应用，属于中档题．
练习册系列答案
相关题目
15．
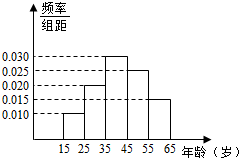某电视台为宣传海南，随机对海南15～65岁的人群抽取了n人，回答问题“东环铁路沿线有哪几个城市？”统计结果如图表所示：
（1）分别求出a，b，x，y的值；
（2）从第2，3，4组回答正确的人中用分层抽样的方法抽取6人，求第2，3，4组每组各抽取多少人？
（3）在（2）抽取的6人中随机抽取2人，求所抽取的人中恰好没有第3组人的概率．
某电视台为宣传海南，随机对海南15～65岁的人群抽取了n人，回答问题“东环铁路沿线有哪几个城市？”统计结果如图表所示：| 组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
| 第1组 | [15，25） | a | 0.5 |
| 第2组 | [25，35） | 18 | x |
| 第3组 | [35，45） | b | 0.9 |
| 第4组 | [45，55） | 9 | 0.36 |
| 第5组 | [55，65） | 3 | y |
（2）从第2，3，4组回答正确的人中用分层抽样的方法抽取6人，求第2，3，4组每组各抽取多少人？
（3）在（2）抽取的6人中随机抽取2人，求所抽取的人中恰好没有第3组人的概率．
5．已知a=2+$\sqrt{3}$，b=1+$\sqrt{6}$，c=$\sqrt{2}$+$\sqrt{5}$，则a，b，c的大小关系为（ ）
| A． | a＞b＞c | B． | c＞a＞b | C． | a＞c＞b | D． | c＞b＞a |
12．设随机变量ξ～N（μ，σ2），函数f（x）=x2+4x+ξ没有零点的概率是0.5，则μ等于（ ）
| A． | 1 | B． | 4 | C． | 2 | D． | 不能确定 |