题目内容
19.已知双曲线$\frac{x^2}{4}+\frac{y^2}{m}=1$的渐近线方程为$y=±\frac{{\sqrt{2}}}{2}x$,则m=-2.分析 利用双曲线$\frac{x^2}{4}+\frac{y^2}{m}=1$的渐近线方程为$y=±\frac{{\sqrt{2}}}{2}x$,可得$\frac{\sqrt{-m}}{2}$=$\frac{\sqrt{2}}{2}$,即可求出m.
解答 解:∵双曲线$\frac{x^2}{4}+\frac{y^2}{m}=1$的渐近线方程为$y=±\frac{{\sqrt{2}}}{2}x$,
∴$\frac{\sqrt{-m}}{2}$=$\frac{\sqrt{2}}{2}$,
∴m=-2.
故答案为:-2.
点评 本题考查双曲线的渐近线,解题的关键是由渐近线方程导出a,b,c的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.如图所示,平面内z1,z2对应的向量分别是$\overrightarrow{OA}$,$\overrightarrow{OB}$,则|z1+z2|=( )
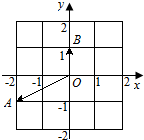

| A. | 2 | B. | 3 | C. | 2 $\sqrt{2}$ | D. | 3 $\sqrt{3}$ |
4.已知集合M={x|0<x<3},N={x|log2x>1},则M∩N=( )
| A. | ∅ | B. | {x|0<x<3} | C. | {x|1<x<3} | D. | {x|2<x<3} |
11.在(2x2-x-1)5的二项展开式中,x的系数为( )
| A. | 10 | B. | -10 | C. | 40 | D. | -40 |
 已知函数$y=sin(ωx+φ)(ω>0,0<φ≤\frac{π}{2})$的部分图象如图所示.
已知函数$y=sin(ωx+φ)(ω>0,0<φ≤\frac{π}{2})$的部分图象如图所示.