14.设数列{an}满足an+1+an-1≤2an(n∈N*,n≥2),则称数列{an}为凸数列,已知等差数列{bn}的公差为lnd,首项b1=2,且数列{$\frac{{b}_{n}}{n}$}为凸数列,则d的取值范围是( )
| A. | (0,e2] | B. | [e2,+∞) | C. | (2,e2] | D. | [2,+∞) |
9.已知函数f(x)=ax(a>0且a≠1)和函数g(x)=sin$\frac{π}{2}$x,若f(x)的反函数为h(x),且h(x)与g(x)两图象只有3个交点,则a的取值范围是( )
| A. | $(\frac{1}{5},1)∪(1,\frac{9}{2})$ | B. | $(0,\frac{1}{7})∪(1,\frac{9}{2})$ | C. | $(\frac{1}{7},\frac{1}{3})∪(5,9)$ | D. | $(\frac{1}{7},\frac{1}{2})∪(3,9)$ |
8.(1-x-3y)5的展开式中不含x的项的系数和为( )
| A. | 32 | B. | -32 | C. | 64 | D. | -64 |
7.直线l:y=kx+1与圆x2+y2=1相交于A,B两点,则“△OAB的面积为$\frac{{\sqrt{3}}}{4}$”是“k=$\sqrt{3}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
6.已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,学校决定利用随机数表法从中抽取100人进行成绩抽样调查,先将800人按001、002、…800编号.
(1)下面摘取了随机数表的第7行到第9行
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 66 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
如果从第8行第7列的数开始向右读,请你依次写出最先检查的5个人的编号;
(2)抽取的100人的数学与地理的水平测试成绩如下表:
成绩分为优秀、良好、及格三个等级;横向、纵向分别表示地理成绩与数学成绩各等级人数,例如:表中数学成绩为良好的共有20+18+4=42.在该样本中,数学成绩优秀率是30%,
在地理成绩及格的学生中,已知a≥10,b≥8,求数学成绩优秀的人数比及格的人数少的概率.
0 247194 247202 247208 247212 247218 247220 247224 247230 247232 247238 247244 247248 247250 247254 247260 247262 247268 247272 247274 247278 247280 247284 247286 247288 247289 247290 247292 247293 247294 247296 247298 247302 247304 247308 247310 247314 247320 247322 247328 247332 247334 247338 247344 247350 247352 247358 247362 247364 247370 247374 247380 247388 266669
(1)下面摘取了随机数表的第7行到第9行
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 66 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
如果从第8行第7列的数开始向右读,请你依次写出最先检查的5个人的编号;
(2)抽取的100人的数学与地理的水平测试成绩如下表:
成绩分为优秀、良好、及格三个等级;横向、纵向分别表示地理成绩与数学成绩各等级人数,例如:表中数学成绩为良好的共有20+18+4=42.在该样本中,数学成绩优秀率是30%,
| 人数 | 数学 | |||
| 优秀 | 良好 | 及格 | ||
地 理 | 优秀 | 7 | 20 | 5 |
| 良好 | 9 | 18 | 6 | |
| 及格 | a | 4 | b | |
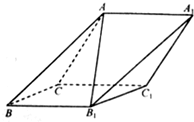 如图,在斜三棱柱 A BC-A1 B1C1中,侧面 ACC1 A1与侧面C B B1C1都是菱形,∠ACC1=∠CC1 B1=60°,AC=2,AB1=$\sqrt{6}$.
如图,在斜三棱柱 A BC-A1 B1C1中,侧面 ACC1 A1与侧面C B B1C1都是菱形,∠ACC1=∠CC1 B1=60°,AC=2,AB1=$\sqrt{6}$.