题目内容
12.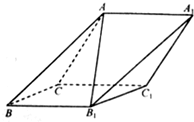 如图,在斜三棱柱 A BC-A1 B1C1中,侧面 ACC1 A1与侧面C B B1C1都是菱形,∠ACC1=∠CC1 B1=60°,AC=2,AB1=$\sqrt{6}$.
如图,在斜三棱柱 A BC-A1 B1C1中,侧面 ACC1 A1与侧面C B B1C1都是菱形,∠ACC1=∠CC1 B1=60°,AC=2,AB1=$\sqrt{6}$.(Ⅰ)求证:平面ACC1A1⊥平面BCC1B1;
(Ⅱ)求二面角C-A B1-A1的余弦值.
分析 (Ⅰ)证明:连AC1,CB1,取CC1中点O,连OA,OB1,证明CC1⊥OA,OA⊥OB1,然后证明OA⊥平面BCC1B1,推出平面ACC1A1⊥平面BCC1B1.
(Ⅱ)分别以OB1,OC1,OA为正方向建立空间直角坐标系,求出平面CAB1的法向量,平面A1AB1的法向量,利用空间向量的数量积求解二面角C-AB1-A1的余弦函数值.
解答 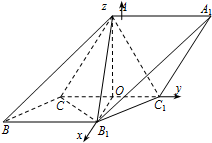 (本小题满分12分)
(本小题满分12分)
解:(Ⅰ)证明:连AC1,CB1,则
△ACC1和△B1CC1皆为正三角形.
取CC1中点O,连OA,OB1,则
CC1⊥OA,且OA=OB1=$\sqrt{3}$,AB1=$\sqrt{6}$
由勾股定理可知OA⊥OB1,∴OA⊥平面BCC1B1,∴平面ACC1A1⊥平面BCC1B1…(5分)
(Ⅱ)解:如图所示,分别以OB1,OC1,OA为正方向建立空间直角坐标系,
则C(0,-1,0),B1($\sqrt{3}$,0,0),A(0,0,$\sqrt{3}$),…(6分)
设平面CAB1的法向量为$\overrightarrow{m}$=(x1,y1,z1),因为$\overrightarrow{A{B}_{1}}$=($\sqrt{3}$,0,-$\sqrt{3}$),$\overrightarrow{AC}$=(0,-1,-$\sqrt{3}$),
所以$\left\{\begin{array}{l}\sqrt{3}{x}_{1}+0×{y}_{1}-\sqrt{3}{z}_{1}=0\\ 0×{x}_{1}-1×{y}_{1}-\sqrt{3}{z}_{1}=0\end{array}\right.$,取$\overrightarrow{m}$=(1,-$\sqrt{3}$,1).…(8分)
设平面A1AB1的法向量为$\overrightarrow{n}$=(x2,y2,z2),因为$\overrightarrow{A{B}_{1}}$=($\sqrt{3}$,0,-$\sqrt{3}$),$\overrightarrow{A{A}_{1}}$=(0,2,0),
所以,$\left\{\begin{array}{l}\sqrt{3}{x}_{2}+0×{y}_{2}-\sqrt{3}{z}_{2}=0\\ 0×{x}_{2}+2×{y}_{2}+0×{z}_{2}=0\end{array}\right.$,取$\overrightarrow{n}$=(1,0,1).…(10分)
则cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{2}{\sqrt{5}×\sqrt{2}}$=$\frac{\sqrt{10}}{5}$,因为二面角C-AB1-A1为钝角,
所以二面角C-AB1-A1的余弦值为-$\frac{\sqrt{10}}{5}$.…(12分)
点评 本题考查二倍角的平面角的求法,平面与平面垂直的判定定理的应用,考查空间想象能力以及计算能力.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案| A. | [-1,$\frac{1}{2}$) | B. | [-2,$\frac{1}{2}$) | C. | [-2,$\frac{3}{2}$) | D. | [-1,$\frac{3}{2}$) |
| A. | c<b<a | B. | c<a<b | C. | b<c<a | D. | b<a<c |
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 开口向上,焦点为(0,1) | B. | 开口向右,焦点为(1,0) | ||
| C. | 开口向上,焦点为(0,$\frac{1}{16}$) | D. | 开口向右,焦点为($\frac{1}{16}$,0) |
| A. | 结论正确 | B. | 大前提不正确 | C. | 小前提不正确 | D. | 全不正确 |