题目内容
9.已知函数f(x)=ax(a>0且a≠1)和函数g(x)=sin$\frac{π}{2}$x,若f(x)的反函数为h(x),且h(x)与g(x)两图象只有3个交点,则a的取值范围是( )| A. | $(\frac{1}{5},1)∪(1,\frac{9}{2})$ | B. | $(0,\frac{1}{7})∪(1,\frac{9}{2})$ | C. | $(\frac{1}{7},\frac{1}{3})∪(5,9)$ | D. | $(\frac{1}{7},\frac{1}{2})∪(3,9)$ |
分析 求出函数的反函数,利用函数的图象的交点推出a的范围即可.
解答 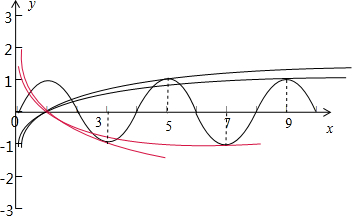 解:函数f(x)=ax(a>0且a≠1),若f(x)的反函数为h(x),
解:函数f(x)=ax(a>0且a≠1),若f(x)的反函数为h(x),
h(x)=logax,
h(x)与g(x)的图象如图:当a>1时,h(x)与g(x)两图象只有3个交点,可得5<a<9;
当0<a<1时,h(x)与g(x)两图象只有3个交点,a∈$(\frac{1}{7},\frac{1}{3})$,
则a的取值范围是:$(\frac{1}{7},\frac{1}{3})∪(5,9)$.
故选:C.
点评 本题考查函数与方程的应用,函数的零点的个数,反函数的应用,考查数形结合以及分类讨论思想的应用,考查计算能力.

练习册系列答案
相关题目
20.已知集合A={1,3,5,7,9},B={0,3,6,9,12},则B∩∁NA=( )
| A. | {6,12} | B. | {3,9} | C. | {0,3,9} | D. | {0,6,12} |
17.设f(x)=$\left\{\begin{array}{l}{4{e}^{x-2}(x<3)}\\{lo{g}_{5}(3x+1)(x≥3)}\end{array}\right.$,则f[f(ln2+2)]=( )
| A. | log515 | B. | 2 | C. | 5 | D. | log5(3e2+1) |
14.设数列{an}满足an+1+an-1≤2an(n∈N*,n≥2),则称数列{an}为凸数列,已知等差数列{bn}的公差为lnd,首项b1=2,且数列{$\frac{{b}_{n}}{n}$}为凸数列,则d的取值范围是( )
| A. | (0,e2] | B. | [e2,+∞) | C. | (2,e2] | D. | [2,+∞) |
 已知椭圆C方程:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),M(x0,y0)是椭圆C上任意一点,F(c,0)是椭圆的右焦点.
已知椭圆C方程:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),M(x0,y0)是椭圆C上任意一点,F(c,0)是椭圆的右焦点.