题目内容
8．（1-x-3y）5的展开式中不含x的项的系数和为（ ）| A． | 32 | B． | -32 | C． | 64 | D． | -64 |
分析 先将问题转化为二项展开式的各项系数和问题，再利用赋值法求出各项系数和．
解答 解：求（1-x-3y）5的展开式中不含x的项的系数和，
即5个多项式（1-x-3y）在展开时全不出x，
（1-x-3y）5的展开式中不含x的项的系数和等于（1-3y）5的各项系数和，
对于（1-3y）5令y=1得展开式的各项系数和为（-2）5=-32，
故选：B．
点评 本题主要考查二项式定理的应用，利用分步乘法将问题等价转化，利用赋值法求展开式的各项系数和，属于基础题．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
3．“${log_a}^x={log_a}^y$（a＞0且a≠1）”是“x=y”的（ ）
| A． | 充要条件 | B． | 充分不必要条件 | ||
| C． | 必要不充分条件 | D． | 既不充分也不必要条件 |
19．已知f（x）=log2$\frac{x+1}{x-1}$（其中x＞1），g（x）=x2-2ax+a2+b（其中x∈R，a＞0，b＞1），则下列判断正确的是（ ）
| A． | f（g（a-1））＞f（g（a）） | B． | f（g（$\frac{2a}{3}$））＞f（g（$\frac{5a}{3}$）） | ||
| C． | g（f（$\frac{{4}^{n}+1}{{4}^{n}-1}$））＞g（f（3））（其中a≠0且a$≠\frac{1}{2}$） | D． | g（f（$\frac{{2}^{n}+1}{{2}^{n}-1}$））＞g（f（3））（其中a≠0，且a≠1） |
16．
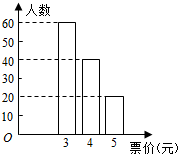2014 年12 月28 日开始，北京市公共电汽车和地铁按照里程分段计价．具体如下表．（不考虑公交卡折扣情况）
已知在北京地铁四号线上，任意一站到陶然亭站的票价不超过5 元，现从那些只乘坐四号线地铁，且在陶然亭出站的乘客中随机选出120 人，他们乘坐地铁的票价统计如图所示．
（Ⅰ）如果从那些只乘坐四号线地铁，且在陶然亭站出站的乘客中任选1 人，试估计此人乘坐地铁的票价小于5 元的概率；
（Ⅱ）从那些只乘坐四号线地铁，且在陶然亭站出站的乘客中随机选2 人，记x 为这2人乘坐地铁的票价和，根据统计图，并以频率作为概率，求X 的分布列和数学期望；
（Ⅲ）小李乘坐地铁从A 地到陶然亭的票价是5 元，返程时，小李乘坐某路公共电汽车所花交通费也是5 元，假设小李往返过程中乘坐地铁和公共电汽车的路程均为s 公里，试写出s 的取值范围．（只需写出结论）
2014 年12 月28 日开始，北京市公共电汽车和地铁按照里程分段计价．具体如下表．（不考虑公交卡折扣情况）| 乘公共汽车方案 | 10公里（含）内2元； 10公里以上部分，每增加1元可乘坐5公里（含） |
| 乘坐地铁方案（不含机场线） | 6公里（含）内3元 6公里至12公里（含）4元 12公里至22公里（含）5元 |
| 22公里至32公里（含）6元 32公里以上部分，每增加1元可乘坐20公里（含） |
（Ⅰ）如果从那些只乘坐四号线地铁，且在陶然亭站出站的乘客中任选1 人，试估计此人乘坐地铁的票价小于5 元的概率；
（Ⅱ）从那些只乘坐四号线地铁，且在陶然亭站出站的乘客中随机选2 人，记x 为这2人乘坐地铁的票价和，根据统计图，并以频率作为概率，求X 的分布列和数学期望；
（Ⅲ）小李乘坐地铁从A 地到陶然亭的票价是5 元，返程时，小李乘坐某路公共电汽车所花交通费也是5 元，假设小李往返过程中乘坐地铁和公共电汽车的路程均为s 公里，试写出s 的取值范围．（只需写出结论）
20．某电信公司从所在地的1000名使用4G手机用户中，随机抽取了20名，对其收集每日使用流量（单位：M）进行统计，得到如下数据：
（1）估计这20名4G手机用户每日使用流量（单位：M）的平均值；
（2）估计此地1000名使用4G手机用户中每日使用流量不少于10M用户数；
（3）在15≤x＜20和20≤x＜25两组用户中，随机抽取两人作进一步问卷调查，求所抽取的两人恰好来自不同组的概率．
| 流量x | 0≤x＜5 | 5≤x＜10 | 10≤x＜15 | 15≤x＜20 | 20≤x＜25 | x≥25 |
| 人数 | 1 | 6 | 6 | 5 | 2 | 0 |
（2）估计此地1000名使用4G手机用户中每日使用流量不少于10M用户数；
（3）在15≤x＜20和20≤x＜25两组用户中，随机抽取两人作进一步问卷调查，求所抽取的两人恰好来自不同组的概率．