13.平行四边形ABCD的对角线AC与BD相交于O,则( )
| A. | $\overrightarrow{AB}$+$\overrightarrow{AD}$=$\overrightarrow{DB}$ | B. | $\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{BC}$ | C. | $\overrightarrow{AB}$+$\overrightarrow{BO}$=$\overrightarrow{OC}$ | D. | $\overrightarrow{AB}$-$\overrightarrow{BC}$=$\overrightarrow{BD}$ |
9.若点$M(a,\frac{1}{b})$和$N(b,\frac{1}{c})$都在直线l:x+y=1上,又点P$(c,\frac{1}{a})$和点$Q(\frac{1}{c},b)$,则( )
| A. | 点P和Q都不在直线l上 | B. | 点P和Q都在直线l上 | ||
| C. | 点P在直线l上且Q不在直线l上 | D. | 点P不在直线l上且Q在直线l上 |
8.在正方体ABCD-A1B1C1D1中,异面直线BC1与CD1所成角的余弦值为( )
| A. | $-\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{2}$ |
7.若点P(x,y)的坐标x,y满足约束条件:$\left\{\begin{array}{l}x+y-6≤0\\ x-y+1≥0\\ x≥1\\ y≥1\end{array}\right.$,则$\frac{3x-4y}{5}$的最大值为( )
| A. | $-\frac{1}{5}$ | B. | -1 | C. | $\frac{11}{5}$ | D. | 11 |
6.数列1,2,1,2,…的通项公式不可能为( )
| A. | ${a_n}=\frac{{3+{{(-1)}^n}}}{2}$ | B. | ${a_n}=\frac{{3+{{(-1)}^{n+1}}}}{2}$ | ||
| C. | ${a_n}=\frac{3+cosnπ}{2}$ | D. | ${a_n}=\frac{{3+sin\frac{2n+1}{2}π}}{2}$ |
5.为了了解城市人均GDP与人均日产生活垃圾量之间的相关关系,国家统计局与卫生管理局随机抽查了6个城市,具体数据如表
(1)计算这6个城市人均日产生活垃圾量的平均值(单位:千克);
(2)求出x与y之间的线性回归方程;
(提供下列参考数据:$\sum_{i=1}^6{x_i}=8.82$,$\sum_{i=1}^6{x_i}{y_i}=8.1$,$\sum_{i=1}^6{x_i}^2=14.7$)
(3)如果某城市的人均GDP达到了3万美元,预测该城市的人均日产生活垃圾量为多少千克?
0 247155 247163 247169 247173 247179 247181 247185 247191 247193 247199 247205 247209 247211 247215 247221 247223 247229 247233 247235 247239 247241 247245 247247 247249 247250 247251 247253 247254 247255 247257 247259 247263 247265 247269 247271 247275 247281 247283 247289 247293 247295 247299 247305 247311 247313 247319 247323 247325 247331 247335 247341 247349 266669
| 城市 | 天津 | 重庆 | 广州 | 深圳 | 武汉 | 西安 |
| 人均GDP(万美元)x | 1.64 | 0.69 | 1.93 | 2.22 | 1.43 | 0.92 |
| 人均日产生活垃圾量(千克)y | 0.64 | 0.51 | 1.05 | 1.15 | 0.99 | 0.76 |
(2)求出x与y之间的线性回归方程;
(提供下列参考数据:$\sum_{i=1}^6{x_i}=8.82$,$\sum_{i=1}^6{x_i}{y_i}=8.1$,$\sum_{i=1}^6{x_i}^2=14.7$)
(3)如果某城市的人均GDP达到了3万美元,预测该城市的人均日产生活垃圾量为多少千克?
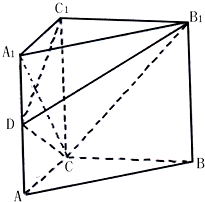 某家居装饰设计的形状是如图所示的直三棱柱ABC-A1B1C1,其中,∠ACB=90°,BCC1B1是边长为2(单位:米)的正方形,AC=1,点D为棱AA1上的动点.
某家居装饰设计的形状是如图所示的直三棱柱ABC-A1B1C1,其中,∠ACB=90°,BCC1B1是边长为2(单位:米)的正方形,AC=1,点D为棱AA1上的动点.