题目内容
10.直线x+y=1与直线2x+2y+m2+2=0间距离的最小值为$\sqrt{2}$.分析 利用两平行线之间的距离公式、二次函数的单调性即可得出.
解答 解:直线2x+2y+m2+2=0化为x+y+$\frac{{m}^{2}+2}{2}$=0,
∴两平行线之间的距离d=$\frac{|\frac{{m}^{2}+2}{2}+1|}{\sqrt{2}}$=$\frac{{m}^{2}+4}{2\sqrt{2}}$$≥\frac{4}{2\sqrt{2}}$=$\sqrt{2}$.当m=0时取等号.
故最小值为:$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查了两平行线之间的距离公式、二次函数的单调性,属于基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
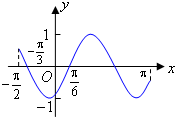
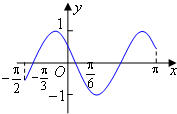
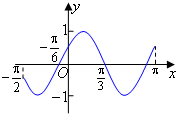
20.以下给出的函数中,以π为周期的奇函数是( )
| A. | y=cos2x-sin2x | B. | y=sin|x| | C. | y=sinx•cosx | D. | y=tan$\frac{x}{2}$ |
5.为了了解城市人均GDP与人均日产生活垃圾量之间的相关关系,国家统计局与卫生管理局随机抽查了6个城市,具体数据如表
(1)计算这6个城市人均日产生活垃圾量的平均值(单位:千克);
(2)求出x与y之间的线性回归方程;
(提供下列参考数据:$\sum_{i=1}^6{x_i}=8.82$,$\sum_{i=1}^6{x_i}{y_i}=8.1$,$\sum_{i=1}^6{x_i}^2=14.7$)
(3)如果某城市的人均GDP达到了3万美元,预测该城市的人均日产生活垃圾量为多少千克?
| 城市 | 天津 | 重庆 | 广州 | 深圳 | 武汉 | 西安 |
| 人均GDP(万美元)x | 1.64 | 0.69 | 1.93 | 2.22 | 1.43 | 0.92 |
| 人均日产生活垃圾量(千克)y | 0.64 | 0.51 | 1.05 | 1.15 | 0.99 | 0.76 |
(2)求出x与y之间的线性回归方程;
(提供下列参考数据:$\sum_{i=1}^6{x_i}=8.82$,$\sum_{i=1}^6{x_i}{y_i}=8.1$,$\sum_{i=1}^6{x_i}^2=14.7$)
(3)如果某城市的人均GDP达到了3万美元,预测该城市的人均日产生活垃圾量为多少千克?
15.已知数列{an}的通项公式为an=2n+3,则( )
| A. | {an}是公比为2的等比数列 | B. | {an}是公比为3的等比数列 | ||
| C. | {an}是公差为2的等差数列 | D. | {an}是公差为3的等差数列 |
19.某超市从2014年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取100个,整理得到数据分组及频率分布表和频率分布直方图:

(Ⅰ)写出频率分布直方图中的a的值,并作出甲种酸奶日销售量的频率分布直方图;
答:a=0.015;
(Ⅱ)记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为s12,s22,试比较s12与s22的大小.(只需写出结论).
答:s12<s22.

| 分组 (日销售量) | 频率 (甲种酸奶) |
| [0,10] | 0.10 |
| (10,20] | 0.20 |
| (20,30] | 0.30 |
| (30,40] | 0.25 |
| (40,50] | 0.15 |
答:a=0.015;
(Ⅱ)记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为s12,s22,试比较s12与s22的大小.(只需写出结论).
答:s12<s22.